Calculation of Sphere Volume
Table of Contents
Volume of a Sphere
A sphere is a 3D object which is shaped like a ball/balloon. It is perfectly symmetrical and all the points on the surface are the same distance (radius) from the center. There are no edges/corners and it has one surface, which can be seen in the diagrams below.
The volume of a sphere is calculated using the equation below:
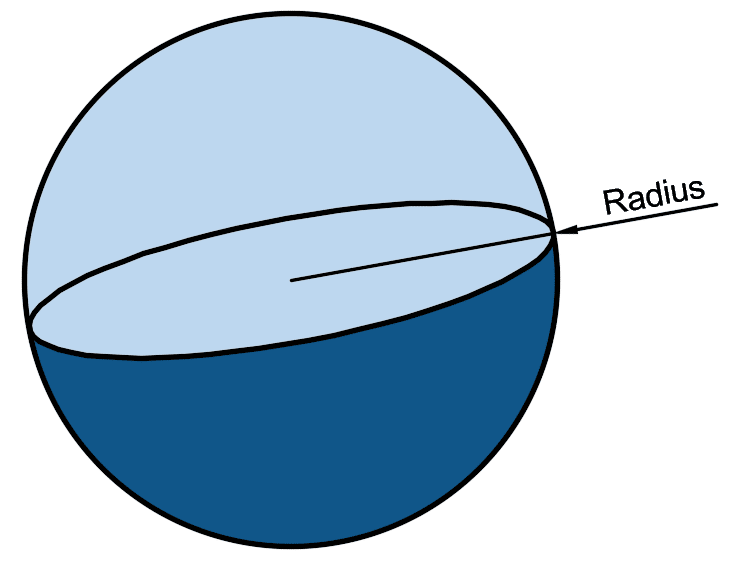
The volume is calculated using the radius of the circle shown on the left.
It is the total amount of space that can fill the spherical object (as the volume increases, so does the surface area).
Imagine a bubble being blown, as we increase the volume of the sphere, the surface area also increases.
A sphere can be divided into two equal parts which are called are hemisphere that passes through the center.
The radius (r) is the distance from the center point of the sphere to the edge of the sphere. The diameter is the radius multiplied by two.
Formula for Volume of a Sphere = \(\frac{4}{3} \pi r^3\)
Volume of a Sphere Example 1
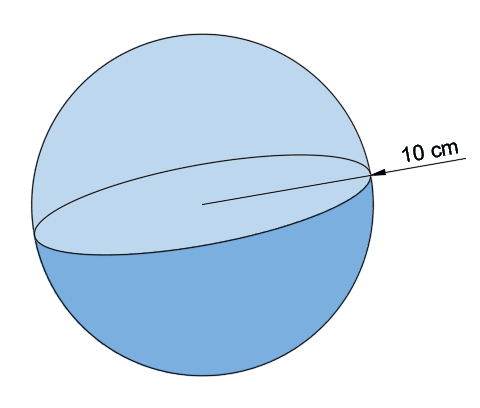
A Sphere has radius of 10 cm. What is the volume of the Sphere?
Solution:
The volume of a sphere formula is \(\frac{4}{3} \pi r^3\)
Volume = \(\frac{4}{3} \pi 10^3\) = 4188 cm3
This can also be written as 0.0042 m3 (4188 multiplied by 10-6 to convert from cm3 to m3).
Note – remember to check units when calculating the volume.
Volume of a Sphere Example 2

A sphere has diameter of 215 mm. What is the volume of the sphere?
Solution:
The volume of a sphere equation is \(\frac{4}{3} \pi r^3\)
The radius is 215/2 = 107.5mm
Volume = \(\frac{4}{3} \pi 107.5^3\) = 5,203,720 mm3
This can also be written as 0.0052 m3 (5,203,720 multiplied by 10-9 to convert from mm3 to m3).
Note – remember to check units when calculating the volume.
