Calculation of Pyramid Volume
Table of Contents
Volume of a Pyramid
A pyramid is a 3D structure with a flat base connected at the top, which is called the apex. There are different types of pyramids such as triangular, square, pentagonal, which refers to the shape of the base.
The volume of a pyramid is the sum total space that can fit inside the pyramid which is enclosed by its base and sides (number of sides depends on the shape of the base).
This article will go over an example calculation for the volume of a square pyramid.
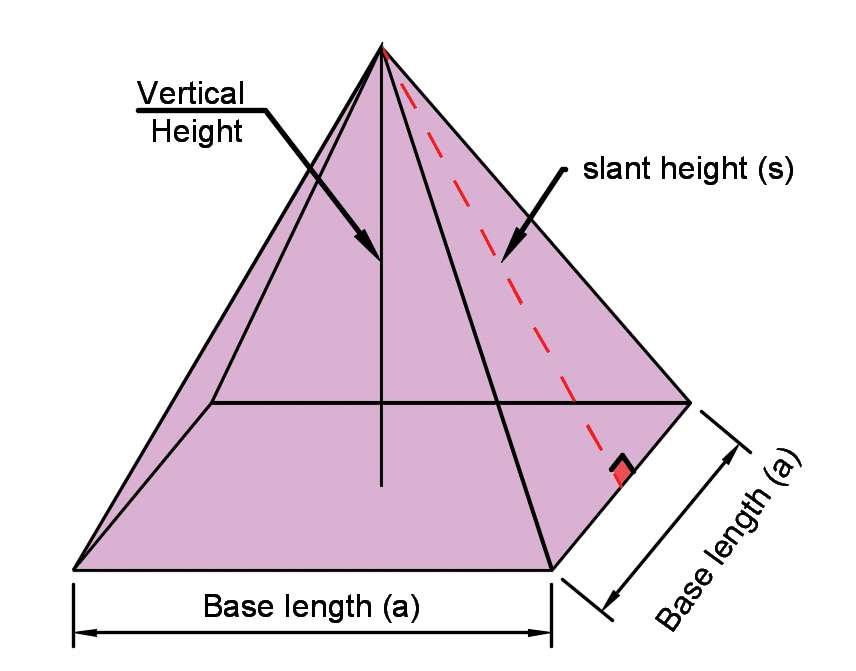
A square shaped pyramid has a square base and triangular faces on each side.
The area of the base will be a x a = a2 (area of square)
The surface area is the sum of the areas of the base and all sides.
a = length of base on each side
h = the height of the pyramid from the centre point of the base to the tip.
Total volume = \(\frac{1}{3} a^2 h\)
Formula for volume of a Pyramid = \(\frac{1}{3} a^2 h\)
Volume of a Square Pyramid Example 1
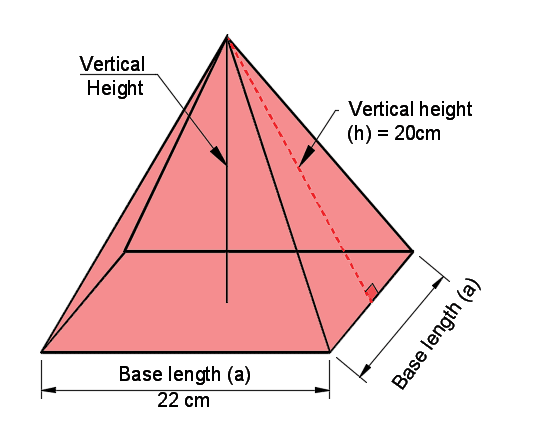
A square pyramid has base length of 22 cm at the base and a vertical height of 20 cm. What is the volume of the pyramid?
Solution:
The volume of a pyramid formula is \(\frac{1}{3} a^2 h\)
Volume = \(\frac{1}{3} 22^2 20\) = 3227 cm3
This can also be written as 0.003227 m3 (3227 multiplied by 10-6 to convert from cm3 to m3).
Note – remember to check units when calculating the volume.
Volume of a Pyramid Example 2
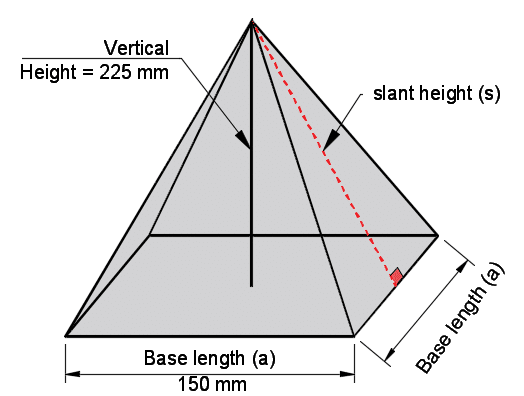
A pyramid has base length of 150 mm at the base and a vertical height of 225 mm. What is the volume of the pyramid?
Solution:
The volume of a pyramid equation is \(\frac{1}{3} a^2 h\)
Volume = \(\frac{1}{3} 150^2 225\) = 1,687,500 mm3
This can also be written as 0.0016875 m3 (1,687,500 multiplied by 10-9 to convert from mm3 to m3).
Note – remember to check units when calculating the volume.
