Calculation of Cone Volume
Table of Contents
Volume of a Cone
A cone is a 3-D structure which has one flat end, and one curved side shown in the example below. The pointed end of a cone is called the apex and the flat end is called the base. The total volume in a cone is the total space that can fit in the cone.
We have different types of cones such as a right angled cone (this is the example in calculations below) and oblique cone (vertex is away from the center of the base).
This article will go over calculation examples for cone volumes using the formula shown below:
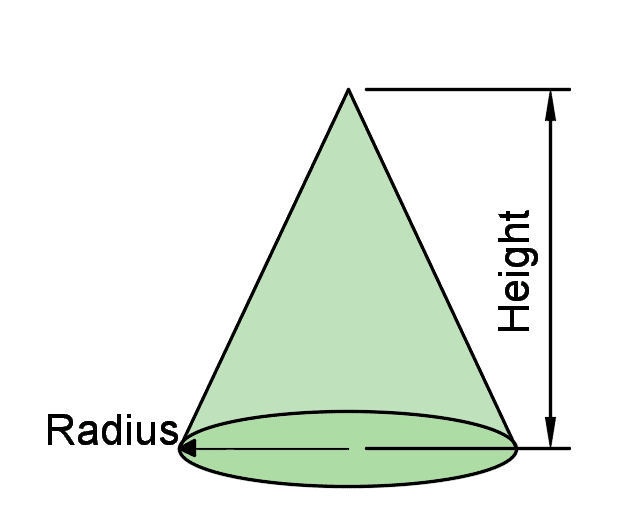
A cone is made up of one curved side and base (circular base). This right angled cone has the apex (tip/point) perpendicular to the base (we can draw a straight line to the center of the flat base).
The area of the base will be πr2 (area of circle).
h = vertical height
r = radius
The total volume of the cone will be \(\frac{\pi}{3} r^2 h\)
Formula for Volume of a Cone = \(\frac{\pi}{3} r^2 h\)
Volume of a Cone Example 1
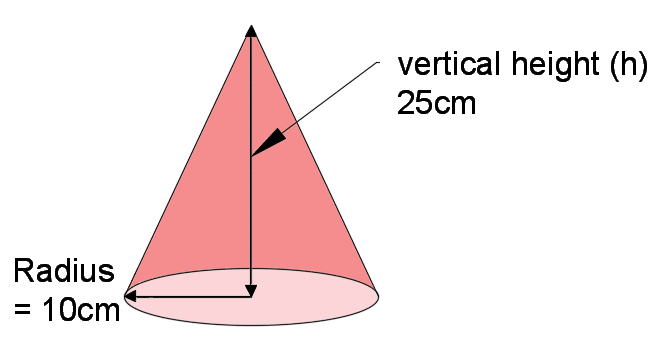
A cone has radius of 10 cm at the base and a vertical height of 25 cm. What is the volume of the cone?
Solution:
The volume of a cone formula is \(\frac{\pi}{3} r^2 h\)
Volume = \(\frac{\pi}{3} 10^2 25\)= 2618 cm3
This can also be written as 0.00262 m3 (1100 multiplied by 10-6 to convert from cm3 to m3).
Note – remember to check units when calculating the Volume.
Volume of a Cone Example 2

A cone has radius of 50 mm at the base and a vertical height of 115 mm. What is the volume of the cone?
Solution:
The volume of a cone equation is \(\frac{\pi}{3} r^2 h\).
Volume = \(\frac{\pi}{3} 50^2 115\) = 301,069 mm3
This can also be written as 0.0301 m3 (301,069 multiplied by 10-9 to convert from mm3 to m3).
Note – remember to check units when calculating the Volume.
