Summary of Beam Deflection Table
Table of Contents
Beam Deflection Formulas
Bending and Deflection Equations
When designing beams (concrete, steel or timber), the bending and shear capacity is checked against applied bending theory.
An applied force causes the element to bend and it is subjected to bending moments and ends react to shear loads.
The bending and shear profile of a beam/element depends on the type of beam support (i.e, pinned, fixed and free ends).
Elastic Beam deflection formula
\(\frac{M}{I}=\frac{\sigma}{y}=\frac{E}{R}\)
- M is the applied moment
- I is the section moment of inertia
- \(\sigma\) is the fibre bending stress
- y is the distance from the neutral axis to the fibre and R is the radius of curvature
- Section modulus is Z=I/y
- Applied bending stress can be simplified to \(\sigma\) = M/Z
KEY Terms in Beam deflection formulas
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
The tables below show beam deflection formulas for simply supported, fixed beam and cantilevers for different end conditions and loadings.
Beam Deflection Formula Tables
Simple Supported Beam Deflection and Formula
Simple Supported Beams under a single Point Load – (2 pin connections at each end)
Note – pin supports cannot take moments, which is why bending at the support is zero.
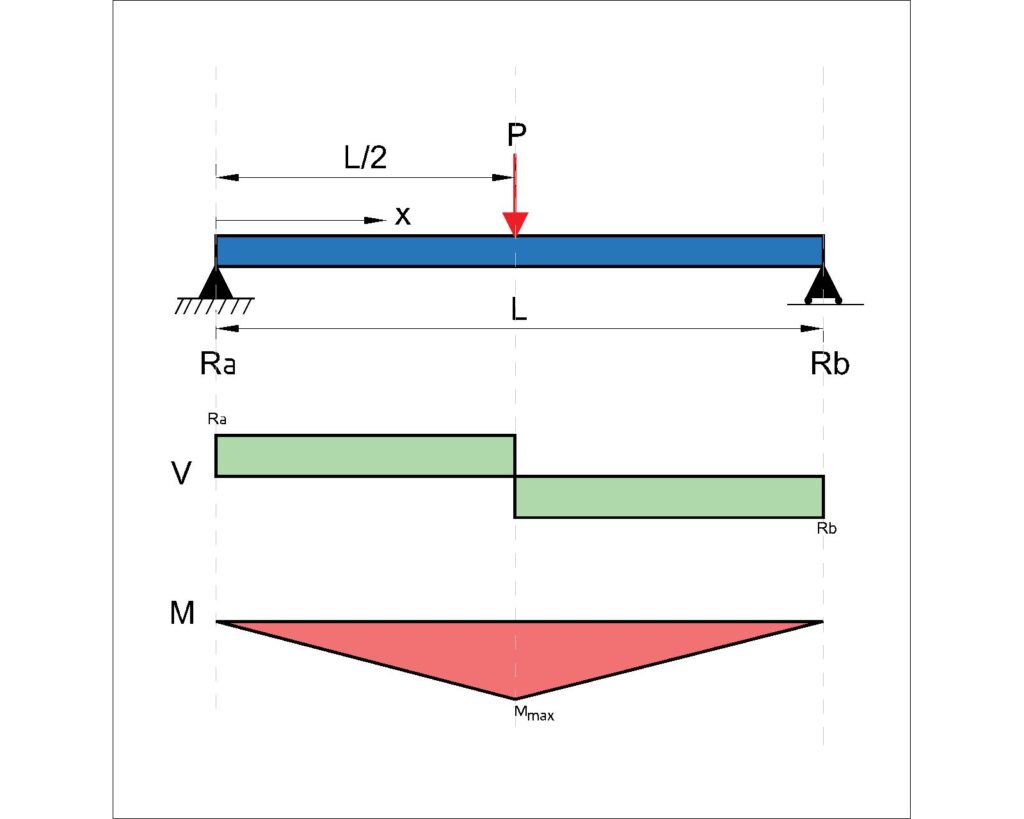
Moment:
\(M_{midspan} = \frac{PL}{4}\)
Beam Deflection Equation:
\(\delta = \frac{PL^3}{48EI}\)
Shear Force and Reaction:
\(R_A=R_B=\frac{P}{2}\)
Simple Supported Beams under a single Point Load located anywhere on the beam – (2 pin connections at each end)
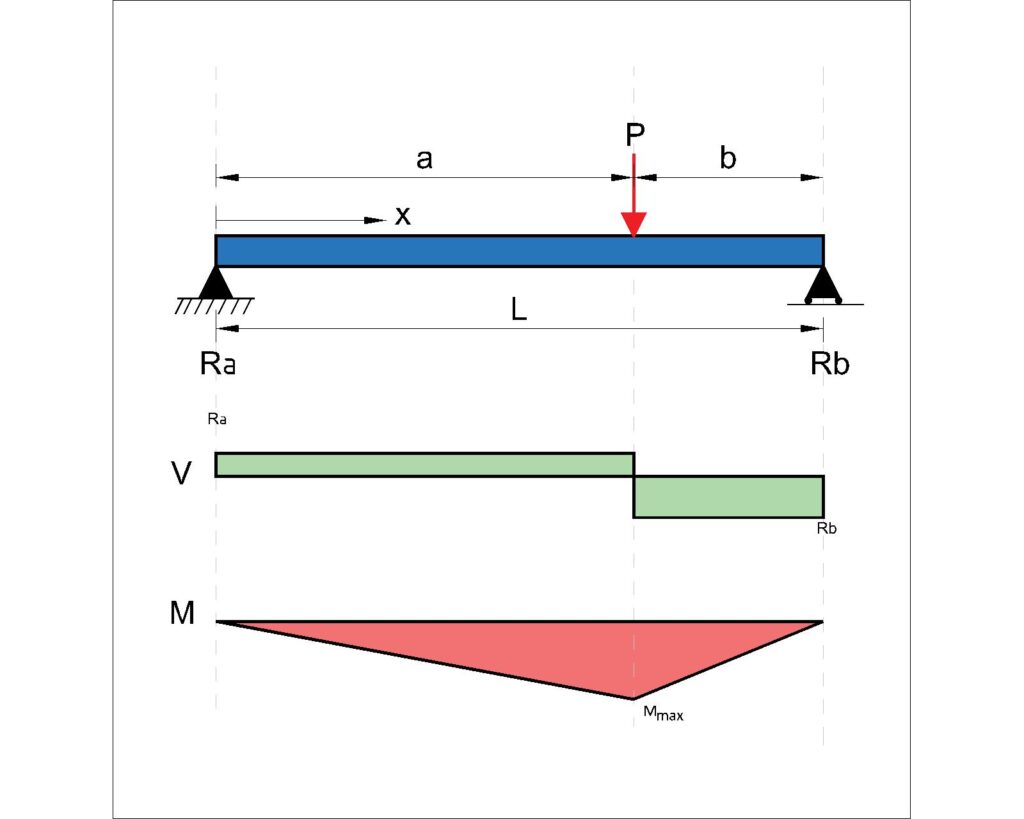
Moment:
\(M_{C} = \frac{Pab}{L}\)
Beam Deflection Equation:
when a>b,
\(\delta_x = \frac{Pab(L+b)}{27EIL} \sqrt{3a(L+b)}\)
at \(x=\sqrt{\frac{a(L+b)}{3}}\) from A
Shear Force and Reaction:
\(R_A= \frac{Pb}{L}\)
\(R_B= \frac{Pa}{L}\)
Simple Supported Beams under a 2 Point Load – (2 pin connections at each end)
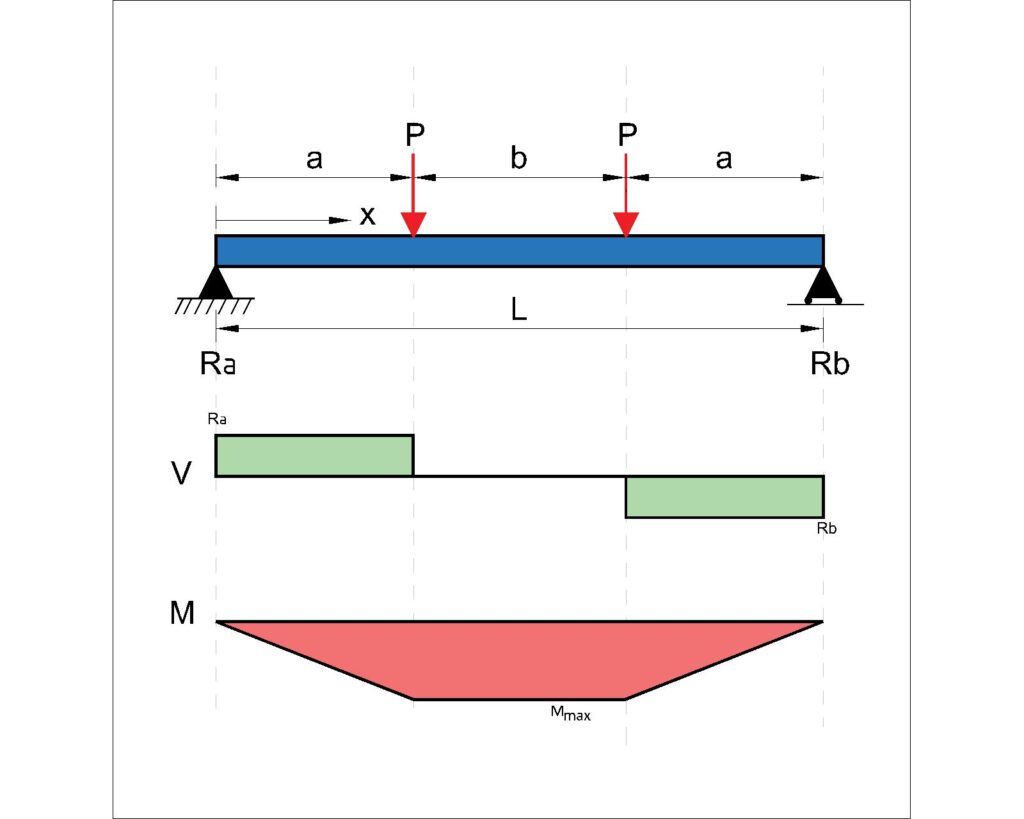
Moment:
\(M_{C} = Pa\)
\(M = \frac{PL}{3}\)
Beam Deflection Equation:
when a>b,
\(\delta_{midspan} = \frac{PL^3}{6EI} (\frac{3a}{4L}-(\frac{a}{L})^3)\)
\(\delta = \frac{23PL^3}{648EI}\)
Shear Force and Reaction:
\(R_A = R_B = P\)
Thirdpoins: \(a=\frac{L}{3}\)
Simple Supported Beams under Uniformly distributed loads (UDL) – (2 pin connections at each end)
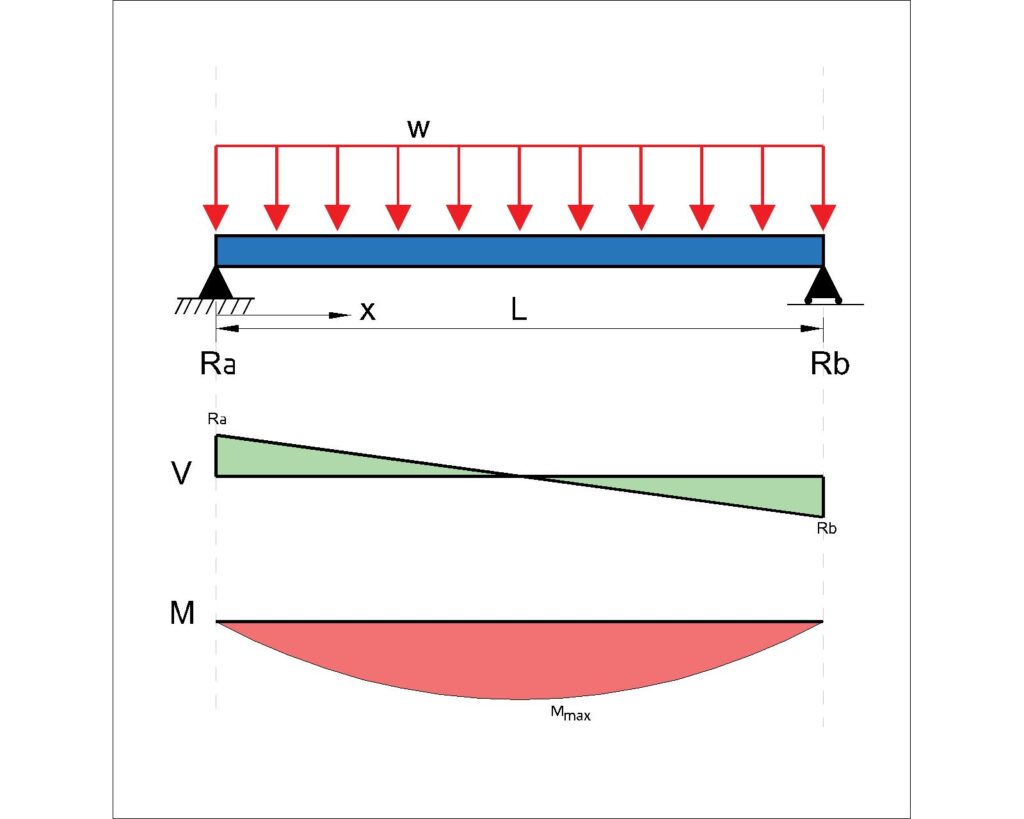
Moment:
\(M_{midpan} = \frac{wl^2}{8}\)
Beam Deflection Equation:
\(\delta_{midspan} = \frac{5wl^4}{384EI} \)
Shear Force and Reaction:
\(R_A = R_B = \frac{wL}{2}\)
Simple Supported Beams under a UDL with cantilever – (2 pin connections with a central pin)

Moment:
\(M_{B} = \frac{wb^2}{2}\)
\(M_{C} = \frac{w(a+b)^2(a+b)^2}{8a^2}\)
maximum x = \(\frac{a}{b}(1-\frac{b^2}{a^2}\)
Beam Deflection Equation:
\(\delta_{c} = \frac{wL}{24EI}(x^4-2ax^3+\frac{2b^2}{a}x^3+a^3x-2ab^2x) \)
\(\delta_{freetip} = \frac{wb}{24EI}(3b^3 + 4ab^2-a^3) \)
Shear Force and Reaction:
\(R_A = \frac{wL}{2a}(a^2-b^2)\)
\(R_B = \frac{wL}{2a}(a^2+b^2)\)
Simple Supported Beams under a VDL load – (2 pin connections at each end)
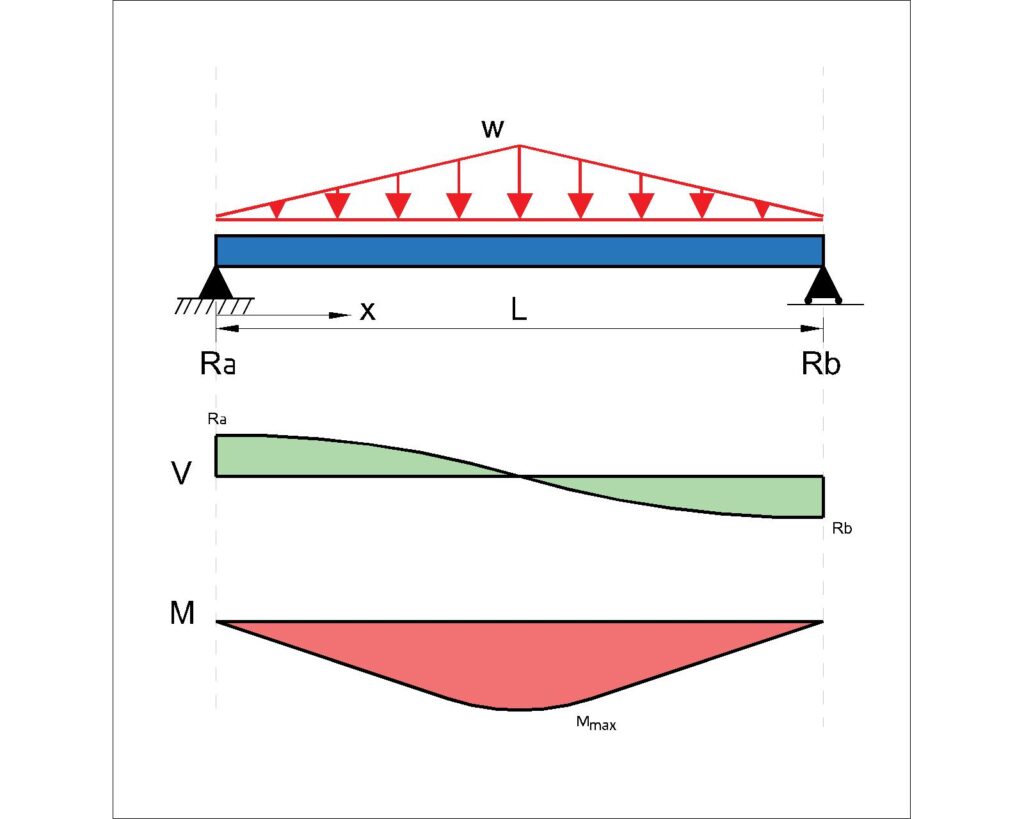
Moment:
\(M_{Midspan} = \frac{WL}{6}\)
Beam Deflection Equation:
\(\delta_{midspan} = \frac{WL^3}{60EI}\)
Shear Force and Reaction:
\(R_A = R_B = \frac{W}{2}\)
Simple Supported Beams under a partial UDL – (2 pin connections at each end)
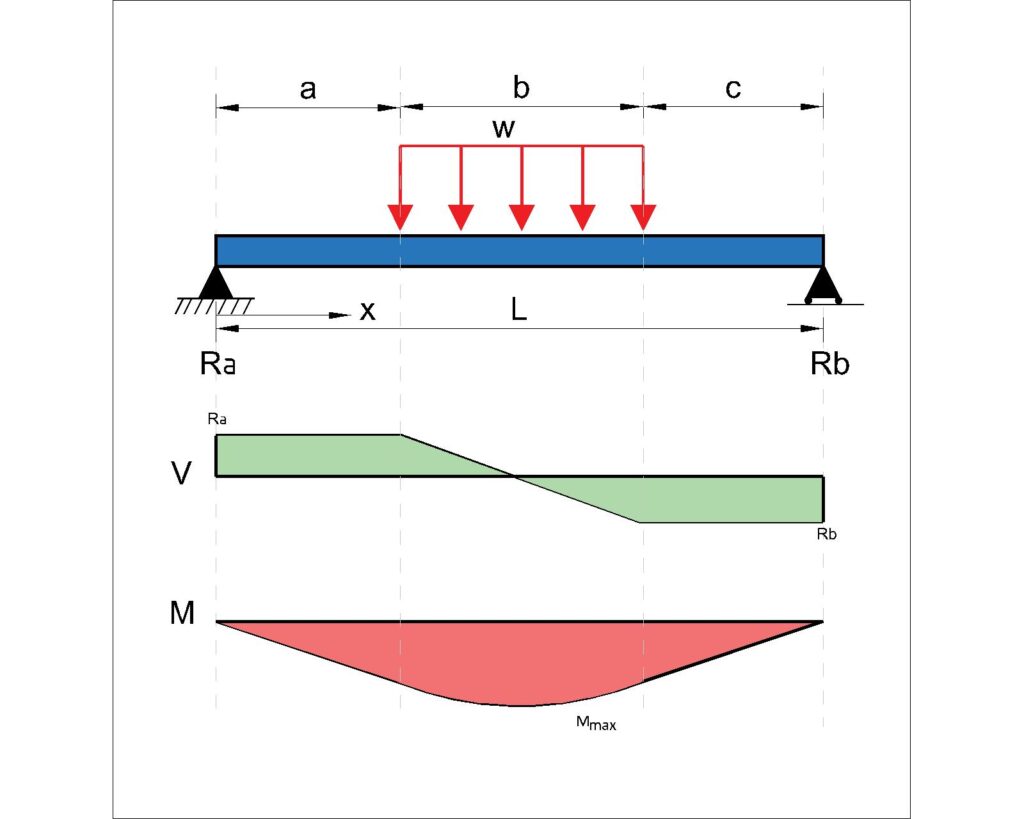
Moment:
\(M_{Max} = \frac{W}{b}(\frac{x_1^2-a^2}{2})\)
When \(x_1=a+\frac{R_Ab}{W}\)
Beam Deflection Equation:
\(\delta_{max} = \frac{W}{384EI}(8L^3-4Lb^2+b^3)\)
Shear Force and Reaction:
\(R_A = \frac{W}{L} (\frac{b}{2}+c)\)
\(R_B = \frac{W}{L} (\frac{b}{2}+a)\)
Fixed Beam Deflection and Formula
Fixed Beams under a single Point Load – (2 fixed connections at each end)
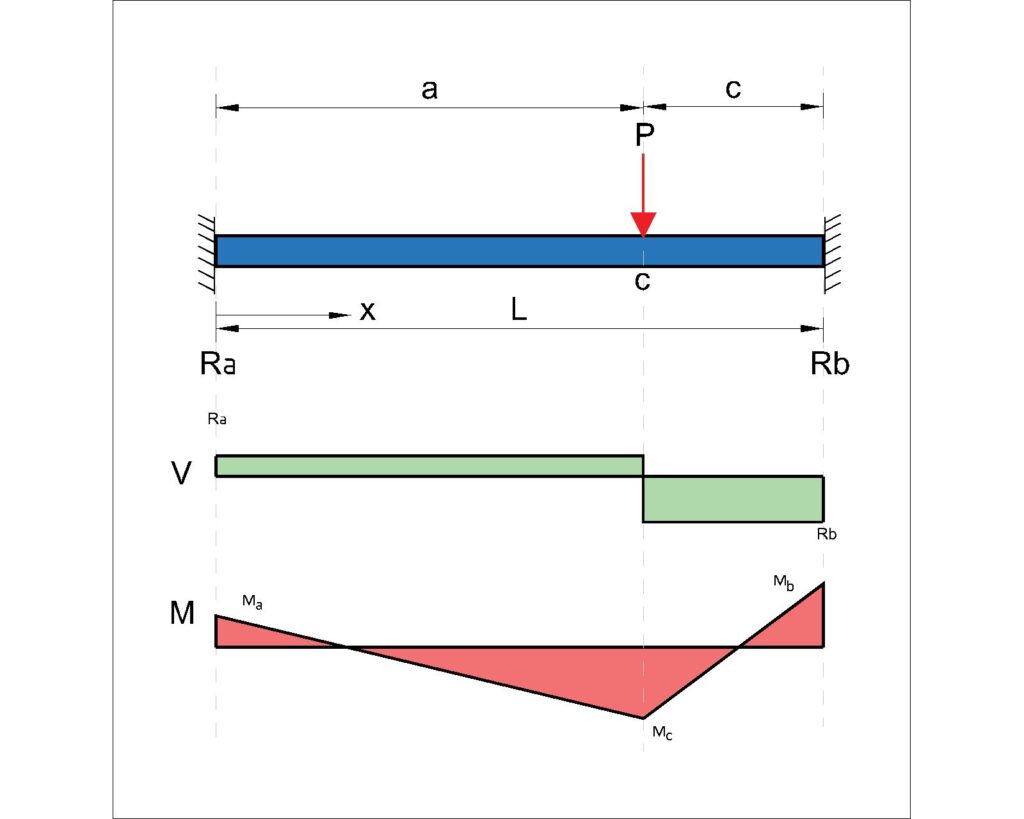
Moment:
\(M_{A} = \frac{-Pab^2}{L^2}\)
\(M_{B} = \frac{-Pba^2}{L^2}\)
\(M_{C} = \frac{2Pa^2b^2}{L^3}\)
Beam Deflection Equation:
\(\delta_{max} = \frac{2Pa^3b^2}{3EI(L+2a)^2}\)
when \(x=\frac{L^2}{(3L-2a)}\)
\(\delta_{c} = \frac{Pa^3b^2}{3EIL}\)
Shear Force and Reaction:
\(R_A = \frac{Pb^2(L+2a)}{L^3}\)
\(R_B = \frac{Pb^2(L+2b)}{L^3}\)
Fixed Beam under UDL – (2 fixed connections at each end)
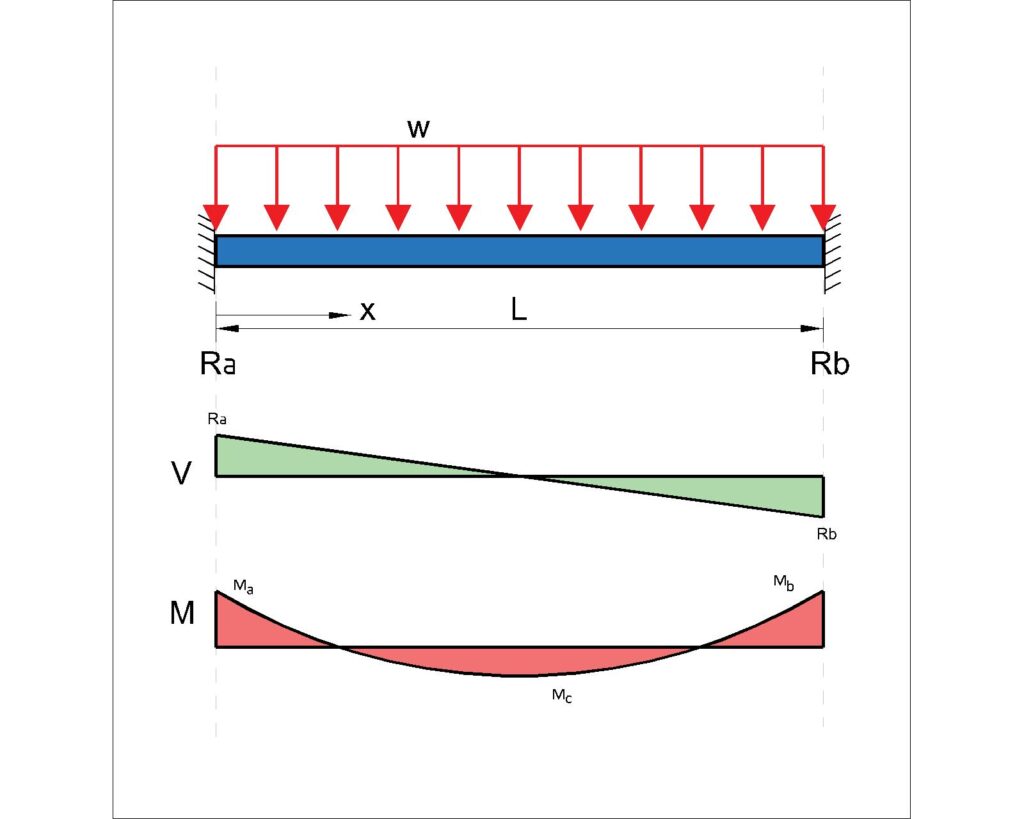
Moment:
\(M_{A} = M_{B} = \frac{-wL^2}{12}\)
\(M_{C} = \frac{wL^2}{24}\)
Beam Deflection Equation:
\(\delta_{midspan} = \frac{wL^4}{384EI}\)
Shear Force and Reaction:
\(R_A = R_B \frac{wL}{2}\)
\(R_A = R_B \frac{wL}{2}\)
Fixed end and pinned with UDL – (1 fixed end and pinned connection at each end).
Note – pin supports cannot take moments, which is why bending at the support is zero.
Note – Fixed supports resists moment, which is why it produces a moment
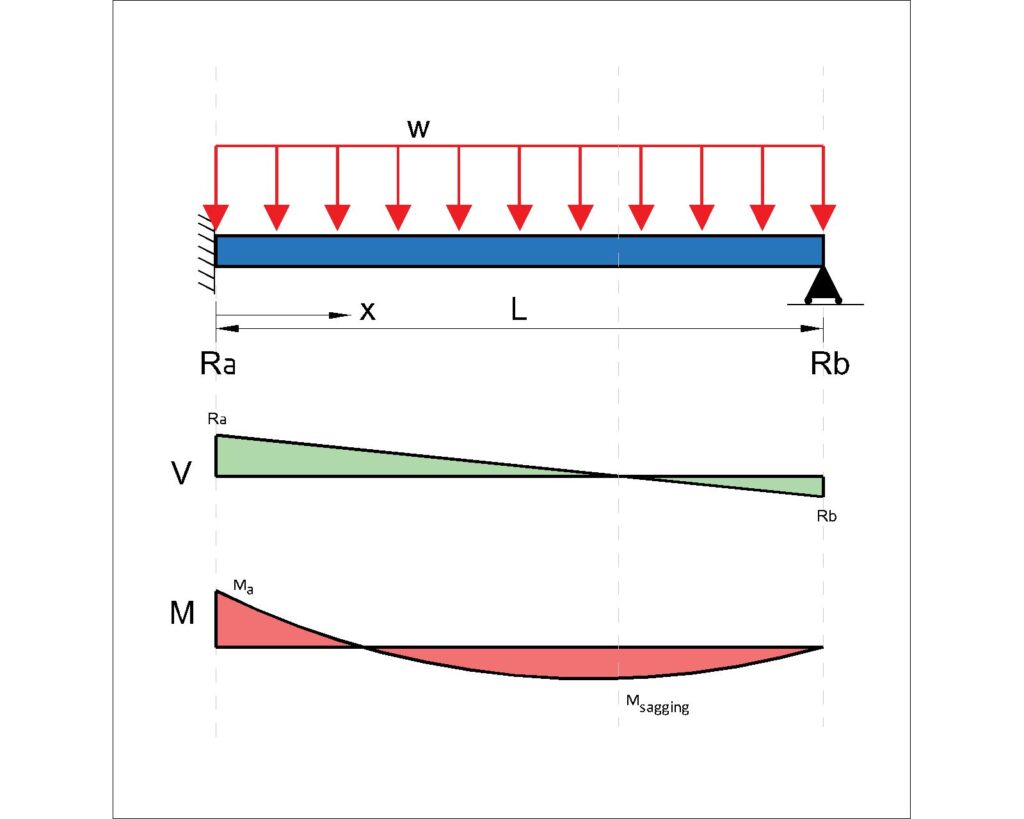
Moment:
\(M_{A} = \frac{-Pb(L^2-b^2)}{2L^2}\)
\(M_{C} = \frac{Pb}{2}(2-\frac{3b}{L}+\frac{b^3}{L^3}\)
Beam Deflection Equation:
\(\delta_{c} = \frac{Pa^3b^2}{12EIL^3}(4L-a)\)
Shear Force and Reaction:
\(R_A = P-R_B\)
\(R_B = \frac{Pa^2(2L+b)}{2L^3}\)
Fixed end cantilever with UDL – (2 pin connections at each end)
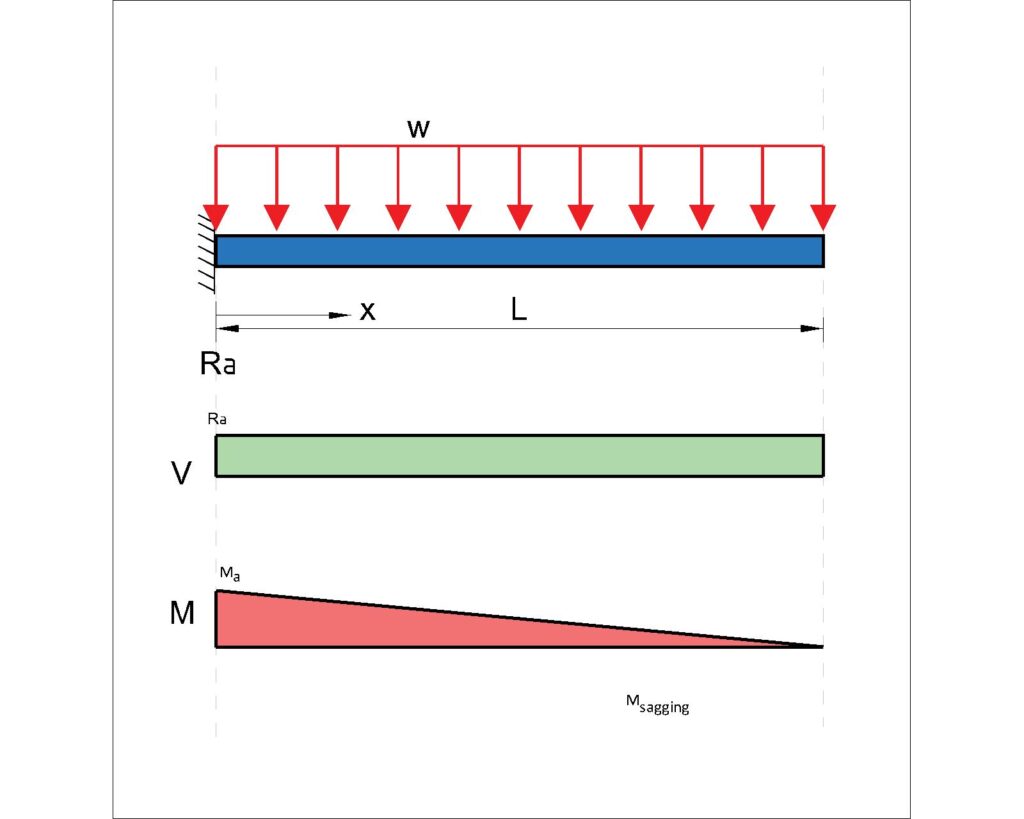
Moment:
\(M_{A} = \frac{-wl^2}{2}\)
Beam Deflection Equation:
\(\delta_{tip} = \frac{WL^3}{8EI}\)
Shear Force and Reaction:
\(R_A = W\)

This Post Has One Comment
Thanks alot …this was very helpful