Concrete Design in Flat Slabs
Table of Contents
What is Punching Shear?
Punching shear is a failure mechanism in flat slabs and foundations, due to concentrated loads causing shear stresses on a section around the load. This type of loading on a slab causes shear failure, which occurs suddenly without any prior warning. Due to this kind of failure, punching shear can cause catastrophic damage and harm to buildings and people. A common example is a column reaction in a slab, which cause punching shear failure in the slab if the shear stress is too high or no shear reinforcement is used in the slab.
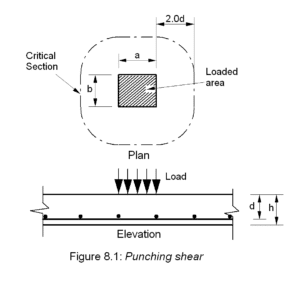
u = the length if the basic control perimeter
d = the effective depth of section of the slab to the two steel layers
Punching Shear Design
There are numerous design techniques to mitigate against punching shear.
- We can use a thicker slab and column increasing the shear capacity.
- Slab with column head
- Slab with column head and drop panels
If the punching shear is very large, then shear reinforcement should be used in the slab, which are usually shear links or stud rails.
If the slab is still inadequate in punching shear, then the structure needs to change, where the applied loading is reduced, slab thickened, reduce grid spacing.
The design effective shear force Veff at the perimeter of the column should be taken as the following:
- = 1.15 VEd for internal columns
- = 1.4 VEd for edge columns
- = 1.5 VEd for corner columns
The maximum shear resistance which can be provided by concrete and bending steel alone (without any steel shear links) can be defined as vRd,c.
vRd,c. = CRd,ck(100\(\rho\)fck)1/3
CRd,c is 0.18/(\gamma_c\) = 0.18/1.5 = 0.12
k = 1+\(\sqrt{}\)200/d \(\leq\)2.0 with d in mm
\(\rho\) is the average percentage of steel
Punching Shear Failure (Pipers Row Car Park)
An example of punching shear failure is the collapse of the Pipers Row car park in Wolverhampton where the 4th floor slab failed under punching shear in 1997. The car park was a 120- tonne concrete structure which was constructed in 1965 and the punching shear failure at one column spread to approximately 8 others.
The structure should have been assessed when the car park structure began to deteriorate through concrete testing, such as core tests to check the strength of concrete. The reinforcement detail should have been checked as well as the shear around the columns, and any defects or corrosion in the structure should have been checked by a competent engineer.
This failure also highlights the importance of progressive collapse in structures. Buildings and structures need to be designed to ensure that a local failure in a structure does not lead to a significant collapse of the structure or whole building. For example, if a single column failed, the building should not collapse and a single column failure should not lead to failure of additional columns or floor plates.

Punching Shear Design Example
A 225mm thick slab (50 year design life) is constructed using C32/40 grade concrete with B16 reinforcement @ 200mm c/c in both directions for residential flats in Manchester. What is the maximum load the slab can take under a 300 x 300mm area load? (This could be applied as a load due to plant equipment or it could be a column reaction)
The first step is to determine the effective depth of the concrete. As the slab is internal and not exposed to outdoor elements in its permanent state; XC1 durability class is chosen. (See table A.4 of BS 8500-1-2015).
A cover of 15 + \(\delta\)c is adopted where \(\delta\) = 15mm. The cover to reinforcement = 30mm.
The effective depth to the reinforcement is \(225 – \frac{16+16}{2}\) = 209mm
The basic control perimeter, u1 = (2a+2b+2\(\pi\) x 2d) = 2(a+ b) + 4\(\pi\)d = 2(300+ 300) + 4\(\pi\)209 = 3826 mm
vRd,c. = CRd,ck(100\(\rho\)fck)1/3
\(\rho\) = As/bd , where Area of steel, As = 1005mm2/m (B16 @ 200mm c/c)
\(\rho\) = 1005/1000 x 209 = 0.0048 (0.48%)
k = 1+\(\sqrt{}\)200/209 = 1.98
vRd,c. = 0.12 x 1.98 (100 x 0.0048 x 32)1/3
vRd,c. = 0.60 N/mm2
VRd,c = 0.60 x 3826 x 209 x 10-3= 480 kN The maximum ultimate point load (300mm x 300mm area) is 480 kN.
The maximum shear force at the face of the loaded area is defined by the equation below:
VRd,max= \(0.5ud[0.6(1-\frac{f_{ck}}{250})]\frac{f_{ck}}{1.5}\)
= 0.5 x (4 x 300) x 209 x [0.6 -(1 -32/250)]32/1.5 x 10-3
= 1866 kN
Therefore, minimum load that the slab can undertake is 480 kN.
