Water Density
Table of Contents
What is the density of water?
The density (specific mass) of a substance is its mass per unit volume. The density of water is approximately 1g/m3 (1 gram per cubic centimeter) or 62 Ib/cu ft (pounds per cubic feet) or 1000 kg/m3 (kilograms per cubic meter) at a temperature of 4°C (39.2 °F), which can also be referred to water density at standard temperature and pressure (STP).
Water density has been taken as 1, as water was used as a standard of measuring the metric unit of mass of other liquids which are measured. Liquids/objects with a density with a density lower than the water density will float when placed in water and objects with a higher density will sink.
The equation for density is defined below:
\(\rho = m/V\)
where
\(\rho\) = density, units are in \(kg/m^3, or Ib/ft^3, or g/cm^3\)
\(m\) = mass, units are in \(kg, or Ib, or g)\)
\(V\) = Volume, units are in \(m^3, or ft^3, or cm^3\)
| Water Density |
| Water density g/cm3 = 1 \(g/cm^3\) |
| Water density g/mL = 1 \(g/mL\) |
| Water density kg/m3 = 1000 \(kg/m^3\) |
| Water density Ibs/ft3= 62.4 \(Ibs/ft^3\) |
Does temperature and pressure affect water density?
Water comprises of hydrogen and oxygen atoms, with a chemical formula of \(H_2O\) and is a unique molecule as water density is affected by temperature when the pressure is constant. Generally, materials are much more dense in their solid state in comparison to their liquid and gaseous states, but ice (water solidified) becomes less dense and floats on water.
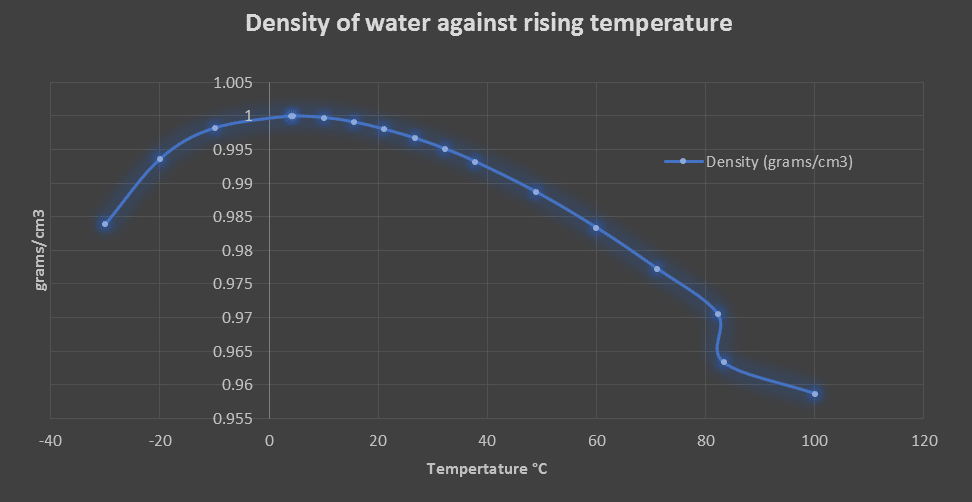
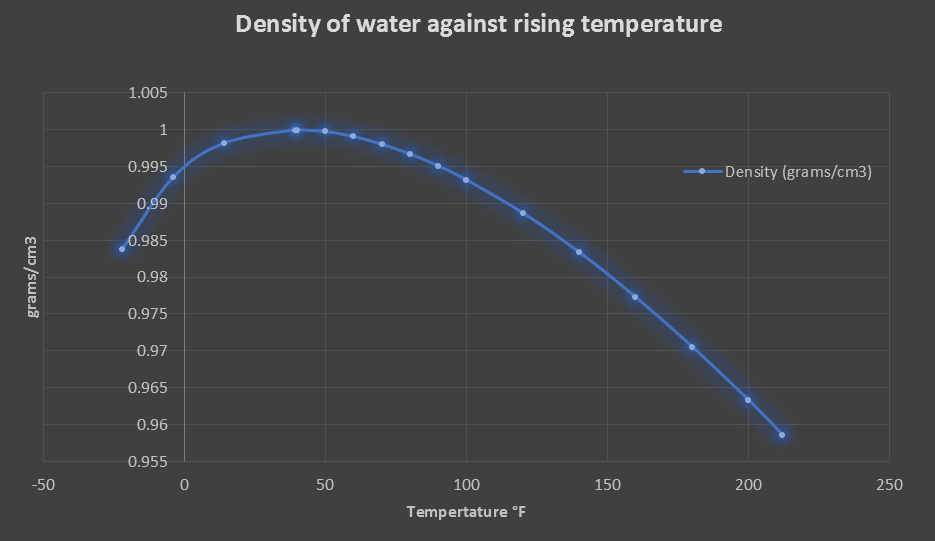
The table below indicates that as the temperature decreases from 100°C (212°F), the density of water increases from 0.95865 to 1.0 \(grams/cm^3\) at a temperature of 4.0°C (39.2 °F), and then the trend reverses and the water density decreases as the temperature go below zero and ice starts to form.
This is why we see icebergs and ice floating in water as they are approximately 9% less dense than water. This is an important when considering the local ecosystem in lakes and rivers. The top layer of a lake begins colder and ice starts to form on the surface. The water that is 4°C is denser than ice and sinks to the bottom of the lake and the water does not solidify and remain. This allows the local plants and animals to survive through the winter months.
| Temperature (°F) | Temperature (°C) | Density (grams/cm3) | Density (kg/m3) | Weight (pounds/ft3) |
| -22°F | -30°C | 0.98385 | 983.85 | 61.42 |
| -4°F | -20°C | 0.99355 | 993.55 | 62.025 |
| 14°F | -10°C | 0.99817 | 998.17 | 62.314 |
| 39.2°F | 4.0°C | 1 | 1000 | 62.424 |
| 40°F | 4.4°C | 0.99999 | 999.99 | 62.423 |
| 50°F | 10°C | 0.99975 | 999.75 | 62.408 |
| 60°F | 15.6°C | 0.99907 | 999.07 | 62.366 |
| 70°F | 21°C | 0.99802 | 998.02 | 62.3 |
| 80°F | 26.7°C | 0.99669 | 996.69 | 62.217 |
| 90°F | 32.2°C | 0.9951 | 995.1 | 62.118 |
| 100°F | 37.8°C | 0.99318 | 993.18 | 61.998 |
| 120°F | 48.9°C | 0.9887 | 988.7 | 61.719 |
| 140°F | 60°C | 0.98338 | 983.38 | 61.386 |
| 160°F | 71.1°C | 0.97729 | 977.29 | 61.006 |
| 180°F | 82.2°C | 0.97056 | 970.56 | 60.586 |
| 200°F | 93.3°C | 0.96333 | 963.33 | 60.135 |
| 212°F | 100°C | 0.95865 | 958.65 | 59.843 |
Examples: Calculating densities of materials and weight of water
Example 1: Calculation of density of concrete in a square box
A square box is being filled with concrete and the dimensions of the box are 2m x 2m x2m. The weight of the concrete is 19200 kg.
Firstly, we need to determine the volume, which is 2 x 2 x 2 = 8m3.
Using the density equation ρ=m/v
19200/8 = 2400 kg/m3 (2.4 g/cm3)
So the density of concrete is 2400 kg/m3.
Example 2: Calculation of weight of water
Calculating the weight of water is important due to the large loadings it can have on a structure. It can appear to be initially negligible, but large volumes can result in large loadings.
For example, calculate the weight of water due to a 10m high water tank, with a plan dimension of 5m x 5m is being filled with pure water and the temperature is 10°C.
What is the density of water? The volume of water is 10m x 5m x 5m = 250m3
The density of water at 10°C is 999.75 kg/m3.
rearranging the density equation ρ=m/v to m =ρ x v
m= 999.75 x 250 = 249937.5 kg or 249.9375 tonnes.
The weight of water is approximately 250 tonnes which is a large amount and can affect engineering applications easily.
Measuring Density of liquid using Hydrometer
A hydrometer is a laboratory measuring device, which is a glass apparatus and measures the density of a liquid. The measuring apparatus is similar to a thermometer with a weighted bulb (usually mercury) at the bottom to make it sit upright. The hydrometer, is put into a cylinder filled up with the liquid to be tested. The position at which the liquid touches the stem of the hydrometer is the relative density of the liquid (measured against a density of water of 1.0).
Hydrometer float lower in less dense liquids and float higher in dense liquids, as water is used as a standard measure with a water density of 1.0. Hydrometers are common in the alcohol industry for measuring the levels of alcohol in spirits or sugar in liquids.