Concrete Design Examples
Table of Contents
One way spanning slabs - Simply supported slab Design
Concrete slabs are either two way spanning or one way spanning slab. A simply supported slab is a type of reinforced concrete slab which is commonly used in construction which is supported on primary beams or a supporting walls. This article will cover a one way spanning slab design example, checking over a reinforcement details.
These can be used for floors, roofs and other engineering applications. A simply supported slab requires more tension reinforcement in the bottom part of the slab as opposed to a continuous slab (due to greater bending moment).
The steps for a one way spanning slab design example is shown below:
- Load take-down on slab
- Preliminary design of slab
- Bending moment reinforcement
- Shear force reinforcement check
- Control crack widths for reinforced concrete
- Span – effective depth ratio
One way spanning slab design example
A simply supported slab is designed to undertake office loading on the first floor .
The office loading has been taken as 2.5 + 1.0 = 3.5 kN/m2. The floor finishes, ceilings and services have been taken as 1.0 kN/m2.
The concrete grade of the slab is C32/40. The fck = 32 N/mm2 and fyk = 500 N/mm2 (yield stress of reinforcement).
Length between slab is 5.0m (centerline of support).
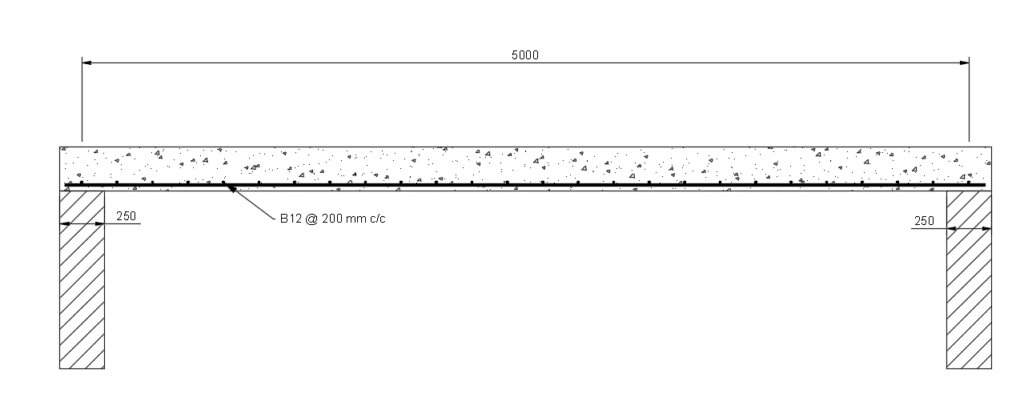
One Way Spanning Slab design Example - Preliminary design
The first step in the design of a simply supported slab is assuming the possible thickness of the slab before undertaking the detailed design. This can be done through basic span/effective depth ratio to determine the basic thickness/depth of the slab.
| Basic ratios of span/effective depth for initial design (f_{yk} = 500 MPa) | |
|---|---|
| Structural System | Span/Effective Depth Ratio |
| Slab | |
| One-way or two-way spanning simply supported slab | 20 |
| End span of: one-way/two-way contnuous spanning slab | 26 |
| Interior span of: one-way/two-way spanning slab | 30 |
| Flat slab (supported on columns) | 24 |
| Cantilever | 8 |
The span/depth ratio = 20 for a simply supported slab.
5000/depth = 20, therefore, 5000/20 = 250mm
Therefore, we will design a 250mm thick slab.
The cover to the slab has been taken as 30mm. (Assume that the slab in internal with an XC1 exposure class). Assume a bar diameter of 12mm.
Effective depth of slab = 250 – 30 – 12/2 = 214mm
Slab Loading
Slab self-weight = 0.25 x 25 kN/m3 = 6.25 kN/m2
Finishes = 1.0 kN/m2
Permanent Load = 7.25 kN/m2
Imposed/Variable Load = 3.5 kN/m2
The slab will be designed in 1m strips
Bending Reinforcement Design
The maximum bending moment for a simply supported slab is wL2/8.
M = wL2/8
M = (1.35 x 7.25 + 1.5 x 3.5) x 5.02/8 = 47 kNm
Bending reinforcement
K = M/bd2fck = (47 x 106)/(1000 x 2142 x 32) = 0.032 < 0.167, no compression is required
From the lever-arm curve, la can be determine or z = d[0.5 + √(0.25-K/1.134)]
\(z = 214[0.5 +\sqrt 0.25 – 0.032/1.134] = 207mm\), check if this is less than 0.95d (0.95 x 214 = 203mm)
\(A_s = \frac{M}{0.87f_{yk}z}\) = (47 x 10^6)/(0.87 x 500 x 203) = 532 mm2/m
Therefore, provide B12 bars @ 150mm c/c, As = 754 mm2.

Shear Design
Shear force occurs at the face of the support.
(1.35 x 7.25 + 1.5 x 3.5) x 5.0 = total force on beam.
Total Force = 75.2 kN
Shear, Ved = 75.2/2 (2.5-0.5 x 0.25/2.5) = 36 kN
Ved/bd = (36 x 103)/(1000 x 214) = 0.168 N/mm2
\(\rho\) = 100 x 754/ (1000 x 214) = 0.352
\(V_{rdc} = v_{rdc}bd\) where
\(v_{rd,c} = [0.12k \times (100 \times \rho \times f_{ck})^{1/3}] \)
where \(K = 1+ \sqrt{200/d}\)
where \(K = 1 + \sqrt{200/214} = 1.97\)
\(v_{rd,c} = [0.12 \times 1.97 \times (100 \times 0.00352 \times 32)^{1/3}] = 0.53 N/mm^2 \)
\(v_{min} = 0.035 \times k^{3/2} \times f_{ck}^{1/2}\)
\(v_{min} = 0.035 \times 1.97^{3/2} \times 32^{1/2} = 0.55 N/mm^2\)
vrdc > ved …OKAY
No shear reinforcement is required
Check Bars Stress
Stress in reinforcement can be checked through the equation below:
\(\sigma_s = \frac{f_{yk}}{\gamma_{ms}} \frac{\psi_2 Q_k + G_k}{1.5Q_k + 1.35 G_k} \frac{A_{s,req}}{A_{s,prov}} \frac{1}{\delta}\)
where \(\psi_2\) can be taken from the table NA.A1.1, which contains values for buildings.
\(\delta\) can be taken as 1.0
\(\frac{f_{ck}}{\gamma_{ms}}\) = 435 for 500 MPa reinforcement.
| Alternative requirements to control crack widths to 0.3mm for members reinforced with high bond bars | |
|---|---|
| Maximum bar diameter (mm) |
Stress range (MPa) |
| 40 | 150-165 |
| 32 | 165-190 |
| 25 | 190-210 |
| 20 | 210-230 |
| 16 | 230-260 |
| 12 | 260-290 |
| 10 | 290-320 |
| 8 | 320-360 |
| Alternative requirements to control crack widths to 0.3mm for members reinforced with high bond bars | |
|---|---|
| Maximum bar spacing (mm) |
Stress range (MPa) |
| 300 | \(\leq\) 160 |
| 275 | 160-180 |
| 250 | 180-200 |
| 225 | 200-220 |
| 200 | 220-240 |
| 175 | 240-260 |
| 150 | 260-280 |
| 125 | 280-300 |
| 100 | 300-320 |
| 75 | 320-340 |
| 50 | 340-360 |
Stress in reinforcement can be checked through the equation below:
\(\sigma_s = 435 \frac{0.7 \times 3.5 + 7.25}{1.5 \times 7.25 + 1.35 \times 3.5} \frac{532}{754} = 190 MPa\)
We can check the 190 MPa on either the two tables. The maximum bar spacing can be taken as 250mm.
We have chosen a bar spacing of 200mm, which is less than 250mm.
Span - effective depth ratio
The actual span/ effective depth = (5000-400)/214 = 21.5
\(\rho = \frac{100A_s}{bd} = \frac{100 \times 754}{1000 \times 214} = 0.35%\)
The allowable span/effective depth from the table below is 30.
\(\frac{A_{s,prov}}{A_{s,req}} = \frac{754}{532} = 1.42\)
The allowable span/effective depth x 1.42 = 30 x 1.42 = 42.6 > 21.5
| Span/effective depth ratios for slabs | |||
|---|---|---|---|
| Location |
\(\frac{A_{s,req}}{bd} \geq 1.5%\) |
\(\frac{A_{s,req}}{bd} = 0.5%\) |
\(\frac{A_{s,req}}{bd} \leq 0.35%\) |
| One-or two way spanning slab: Simply supported End span Interior span |
|||
| 14 | 20 | 30 | |
| 18 | 26 | 39 | |
| 20 | 30 | 45 | |
| Flat slab | 17 | 24 | 36 |
| Cantilever | 6 | 8 | 12 |
