Civil's Guide
Masonry Design
Design Strength of Masonry
Masonry can be designed using Eurocode 6 and its strength is determined by the equation below:
\(f_d=\frac{f_k}{\gamma_m}\)
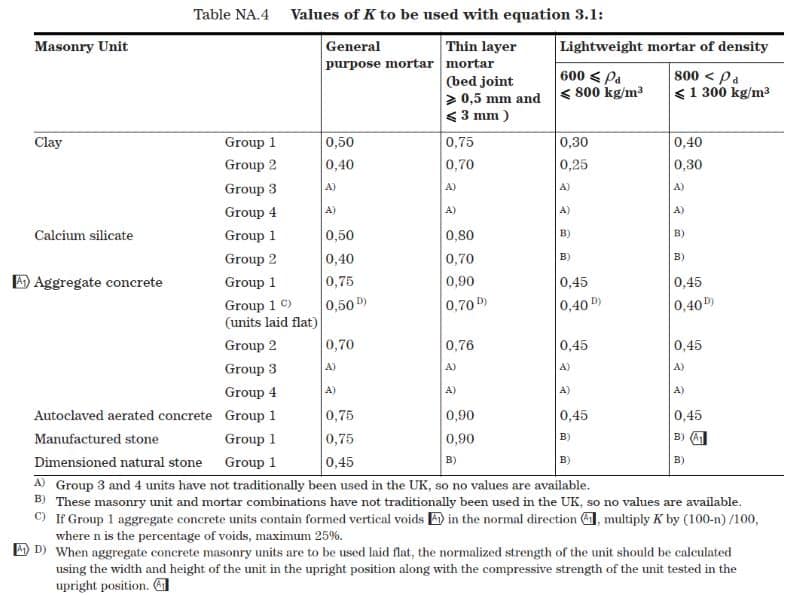
where \(f_k = Kf_b^af_b^\beta\)
- \(f_k\) = is the characteristic strength o fmasonry, in N/mm2
- K is a constant (related to clay type)
- \(\alpha,\beta\) are constants (related to mortar)
- \(f_b\) is the normalised mean compressive strength of the units, in the direction of the applied action effect, in N/mm2
- \(f_m\) is the compressive strength of the mortar, in N/mm2
- \(\gamma_m\) is the partial factor for the material
Values of \(\alpha\) and \(\beta\)
Values of K
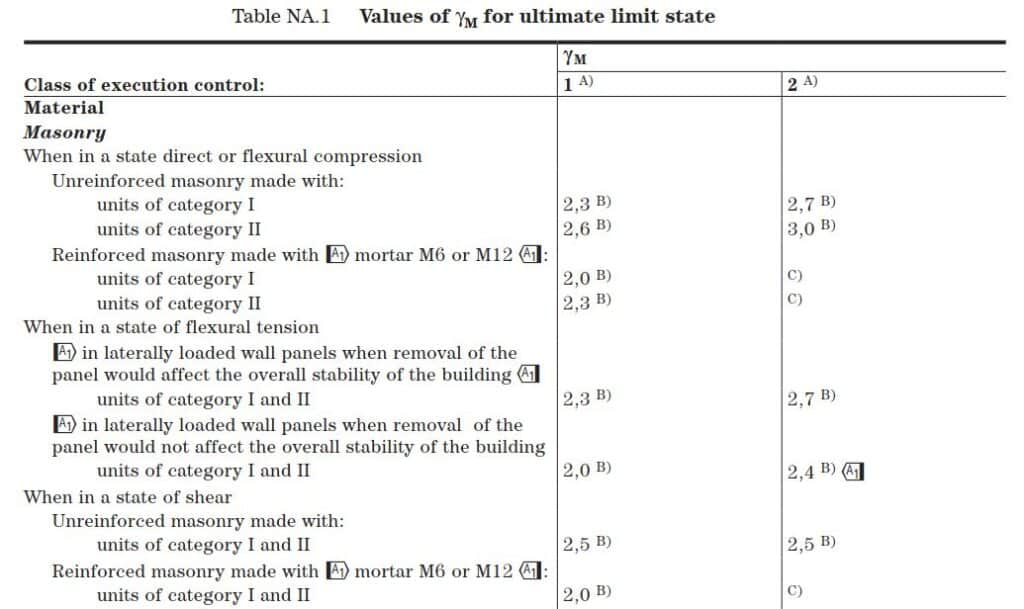
Category and Execution Control Class
Masonry units of Category I (probably of failure not exceeding 5%) are made under stricter quality control conditions than Category II.
Execution Control Class 2:
–All work on site properly supervised and carried out in accordance with EC6 Part 2 with attention to:
–Setting out
–Storage
–Batching, mixing and use of mortar
–Laying of masonry units
–Construction details
–Protection during construction
Execution Control Class 1:
As above. In addition, the work is properly inspected and mortar is regularly sampled and tested for strength.
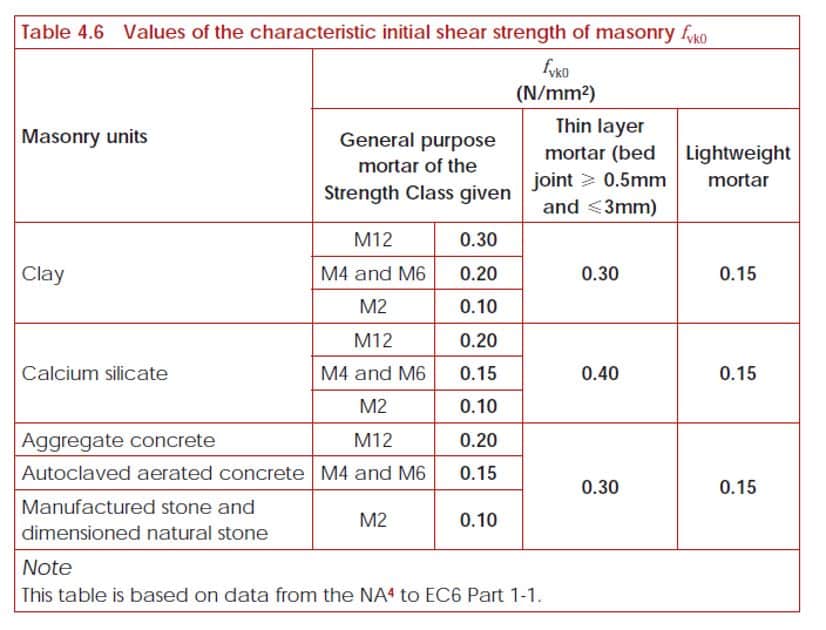
\(f_{vk}\) – Characteristic Shear Strength of Masonry
The characteristic shear strength of masonry \(f_{vk}\) depends upon the characteristic initial shear strength of the masonry \(f_{vk0}\) (obtained from tests, table 3.4 of EC6 part 1-1) and the design compressive stress perpendicular to the shear plane, at the level concerned, \(\sigma_d\).
The characteristic shear strength is given by:
\(f_{vk}=f_{vk0}+0.4\sigma_d\) for fully filled joints
\(f_{vk} = 0.5 f_{vk0} + 0.4 \sigma_d\) for unfilled perpend joints
where: \(f_{vk0{\) is the characteristic initial shear strength, under zero compressive strength
\(\sigma_d\) is the design compressive stress perpendicular to the shear in the member at the level under consideration using the appropriate load combination based on the average vertical stress over the compressed part of the wall that is providing shear resistance.
\(f_{vko}\) – Characteristic Shear Strength of Masonry
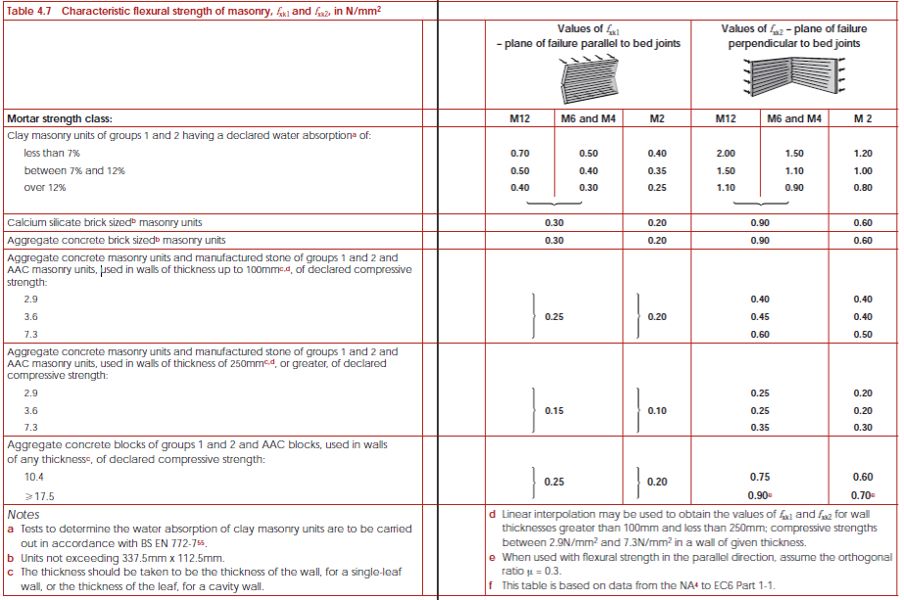
Characteristic Flexural Strength of Masonry: \(f_{xk1}\) and \(f_{xk2}\)
Ultimate Flexural strength of an uncracked wall spanning horizontally
\(M_{Rd2} = \frac{f_{kx2}}{\gamma_m}Z\) (perpendicular to bed joints)
Ultimate Flexural strength of an uncracked wall spanning Vertically
\(M_{Rd1} = (\frac{f_{kx1}}{\gamma_m}+0.9G)Z\) (parallel to bed joints)
Ultimate Flexural strength of an cracked wall spanning vertically
\(M_{Rd1} = \frac{\gamma_wf^2h}{2\gamma_f}\)Z
