Summary of Masonry Properties
Table of Contents
What is Masonry ?
Masonry is a common building material which refers to the individual units which are laid and bound together by mortar. It is often used for walls of buildings as seen in many parts of the world as it is good in compression but has limited flexural strength.
The main components of any masonry building are found below:
- Masonry Units
- Mortar
- Wall ties
- Damp proof courses
- Reinforcement
Types of masonry units
- Clay bricks – BS EN 771-1:
–Clay, or other argillaceaous material, fired at sufficiently high temperature to achieve a ceramic bond.
- Calcium silicate – BS EN 771-2:
–Lime and sand hardened by high-pressure steam.
- Aggregate concrete blocks – BS EN 771-3:
–Lightweight or normal weight concrete
- Autoclaved aerated concrete blocks – BS EN 771-4:
–Low density blocks, low strength, but good thermal resistance
- Manufactured stone – BS EN 771-5:
–Concrete units made to resemble natural stone
- Natural stone – BS EN 771-6:
–Natural stone cut to required shape. Properties determined by tests
Types of Bricks
There are literally thousands of different bricks – reduce basic types. The vast majority are made from clay and are kiln-fried.
Facing Bricks
Quality, durable bricks with an attractive appearance for external use above ground.
Wirecut
The clay is continuously extruded to a required size and shape and then cut into individual bricks by means of awire. Usually the cheapest facings available since the manufacturing process is highly automated.
Engineering
The workhorses of the brick family. Tough, strong, hard-wearing but not usually very pretty. Excellent resistance to frost & water, ideal for groundworks, sewer works, retaining walls.
Clay bricks
Clay brick densities range from 22 – 28 kN/m3 and be either hand made or factory made.
Engineering bricks is defined by 2 categories
- Class A strength > 70 N/mm2; water absorption < 4.5% by mass.
- Class B strength > 50 Nmm2; water absorption < 7.0% by mass.
Calcium Silicate Bricks
This type of brick is popular in areas where good brick making clay is scarce and a lot cheaper in comparison. Densities are lower and range from 17-21 kN/m3.
Concrete Blocks
These are cement bound blocks which has a high range of densities depending on what aggregates are used. The density ranges from 5 to 20 kN/m3
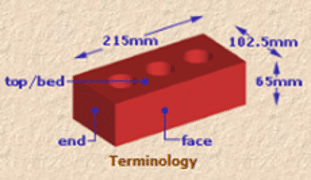
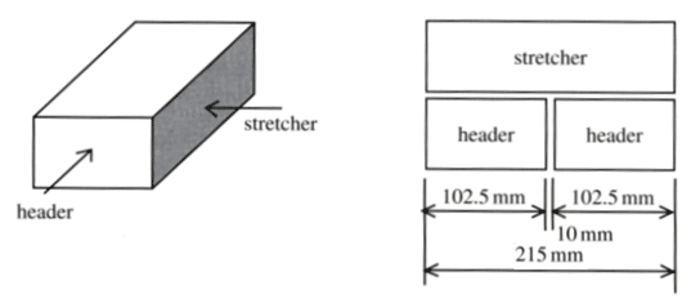
Brick Dimensions
The UK modular format: standard brick size 215×102.5×65 mm (face x bed x end). With a standard 10 mm wide joint, gives a working size of 225mm x 75 mm.
4 courses of bricks (+bedding joints) gives a total depth of 300 mm. 4 bricks in a line gives a width of 900mm including the perpends (vertical joints)
Using stretcher bond, there are 60 bricks/m2 in a single skin wall.
Cement mortar mixes for masonry
| Compressive Strength class | Compressive strength \(f_m\) | Mortar class | Mortar constituents and proportions | |||
|---|---|---|---|---|---|---|
| Cement:Lime:Sand | Cement:Sand | Masonry \(Cement^a\):Sand | Masonry \(Cement^b\):Sand | |||
| M12 | 12 N/mm2 | (i) | 1:0:3 to 1:\(\frac{1}{4}\):3 | 1:3 | ||
| M6 | 6 N/mm2 | (ii) | 1:\(\frac{1}{2}\):4 to 1:\(\frac{1}{2}\):4\(\frac{1}{2}\) | 1:3 to 1:4 | 1:2\(\frac{1}{2}\) to 1:3\(\frac{1}{2}\) | 1:3 |
| M4 | 4 N/mm2 | (iii) | 1:1:5 to 1:1:6 | 1:5 to 1:6 | 1:4 to 1:5 | 1:3\(\frac{1}{3}\) to 1:4 |
| M2 | 2 N/mm2 | (iv) | 1:1:8 to 1:1:9 | 1:7 to 1:8 | 1:5\(\frac{1}{2}\) to 1:6\(\frac{1}{2}\) | 1:4\(\frac{1}{2}\) |
Movement joints in brickwork
| Material | Approximate horiozntal joint spacing and reason for provision | Typical joint thickness (mm) | Maximum suggested panel length: Height ratio |
|---|---|---|---|
| Clay bricks | 12m for expansion | 16 | 3:1 |
| 15-18m with bed joint reinforcement at 450 mm c/c | 22 | ||
| M12 | 18-20m with bed joint reinforcement at 225 mm c/c12 N/mm2 | 25 | |
| Calcium silicate bricks | 7.5 – 9 m for shrinkage | 10 | 3:1 |
| Concrete blocks | 6-7m for shrinkage | 10 | 2:1 |
| 15-18m with bed joint reinforcement at 450 mm c/c | 22 | ||
| 18-20m with bed joint reinforcement at 225 mm c/c | 25 | ||
| Natural stone cladding | 6m for thermal movements | 10 | 3:1 |
Masonry Design Equations
Design Strength of Masonry
Masonry can be designed using Eurocode 6 and its strength is determined by the equation below:
\(f_d=\frac{f_k}{\gamma_m}\)
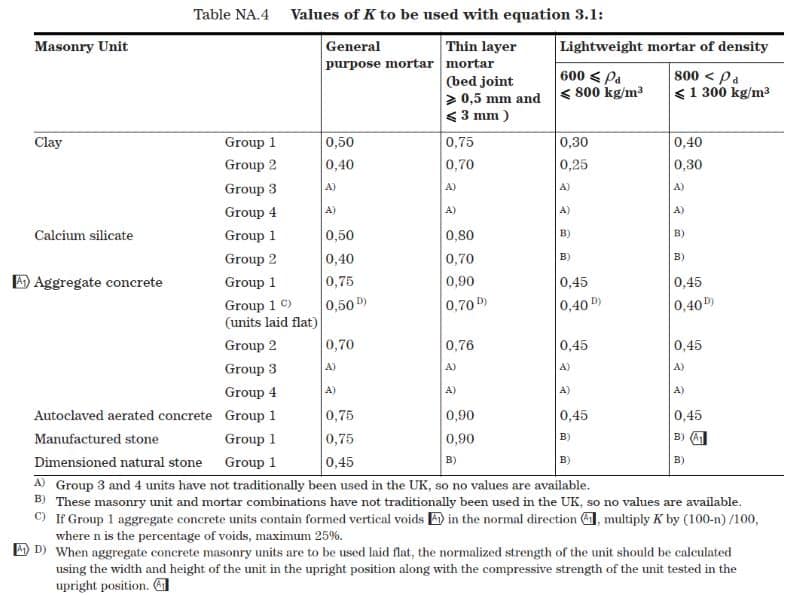
where \(f_k = Kf_b^af_b^\beta\)
- \(f_k\) = is the characteristic strength o fmasonry, in N/mm2
- K is a constant (related to clay type)
- \(\alpha,\beta\) are constants (related to mortar)
- \(f_b\) is the normalised mean compressive strength of the units, in the direction of the applied action effect, in N/mm2
- \(f_m\) is the compressive strength of the mortar, in N/mm2
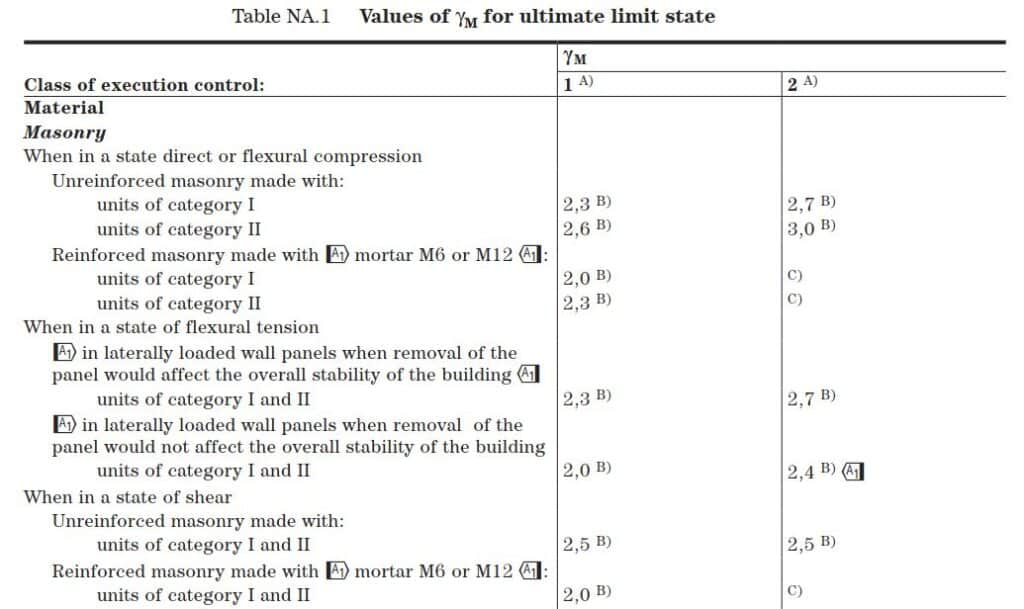
- \(\gamma_m\) is the partial factor for the material
Values of \(\alpha\) and \(\beta\)
Values of K
Category and Execution Control Class
Masonry units of Category I (probably of failure not exceeding 5%) are made under stricter quality control conditions than Category II.
Execution Control Class 2:
–All work on site properly supervised and carried out in accordance with EC6 Part 2 with attention to:
–Setting out
–Storage
–Batching, mixing and use of mortar
–Laying of masonry units
–Construction details
–Protection during construction
Execution Control Class 1:
As above. In addition, the work is properly inspected and mortar is regularly sampled and tested for strength.
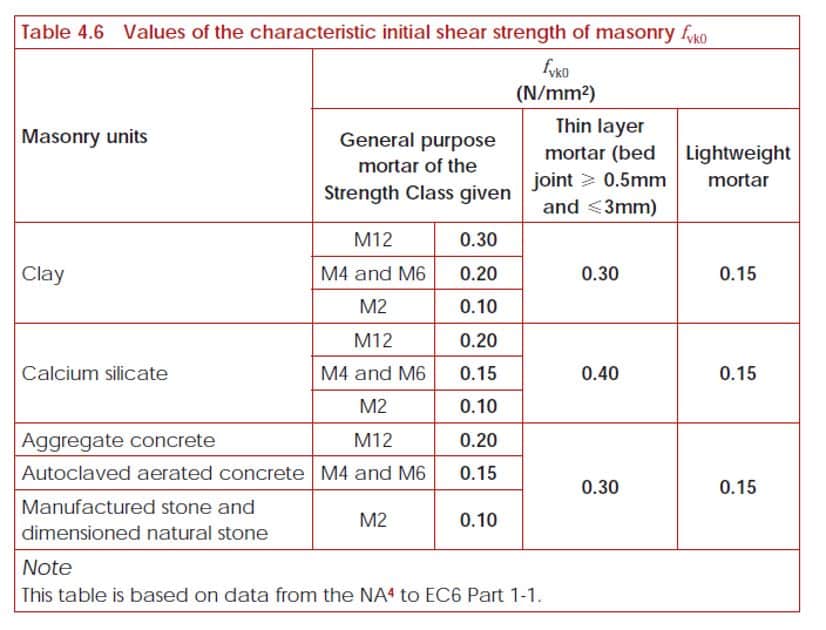
\(f_{vk}\) – Characteristic Shear Strength of Masonry
The characteristic shear strength of masonry \(f_{vk}\) depends upon the characteristic initial shear strength of the masonry \(f_{vk0}\) (obtained from tests, table 3.4 of EC6 part 1-1) and the design compressive stress perpendicular to the shear plane, at the level concerned, \(\sigma_d\).
The characteristic shear strength is given by:
\(f_{vk}=f_{vk0}+0.4\sigma_d\) for fully filled joints
\(f_{vk} = 0.5 f_{vk0} + 0.4 \sigma_d\) for unfilled perpend joints
where: \(f_{vk0{\) is the characteristic initial shear strength, under zero compressive strength
\(\sigma_d\) is the design compressive stress perpendicular to the shear in the member at the level under consideration using the appropriate load combination based on the average vertical stress over the compressed part of the wall that is providing shear resistance.
\(f_{vko}\) – Characteristic Shear Strength of Masonry
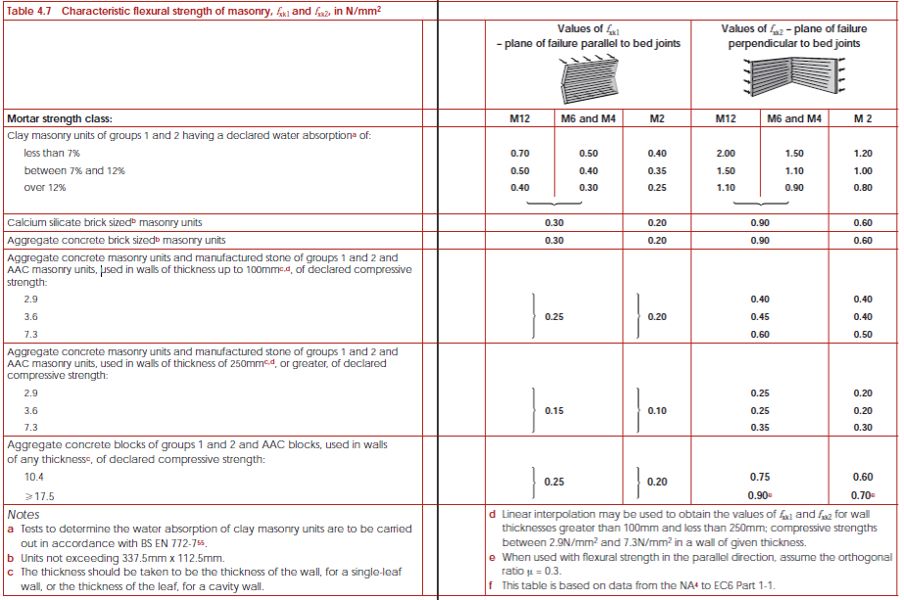
Characteristic Flexural Strength of Masonry: \(f_{xk1}\) and \(f_{xk2}\)
Ultimate Flexural strength of an uncracked wall spanning Vertically
\(M_{Rd1} = (\frac{f_{kx1}}{\gamma_m}+0.9G)Z\) (parallel to bed joints)
Ultimate Flexural strength of an uncracked wall spanning horizontally
\(M_{Rd2} = \frac{f_{kx2}}{\gamma_m}Z\) (perpendicular to bed joints)
Ultimate Flexural strength of an cracked wall spanning vertically
\(M_{Rd1} = \frac{\gamma_wf^2h}{2\gamma_f}\)Z
