Concrete Beam Design to BS EN 1992-1-1
Table of Contents
How to Design a concrete beam in simple steps - Bending reinforcement
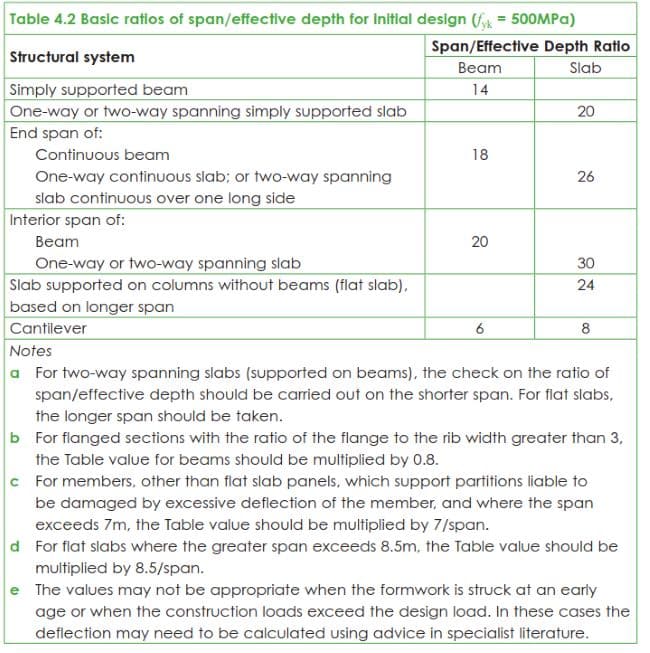
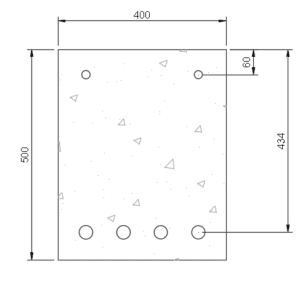
Beam shown below is a simply supported beam, where span is taken as 6250mm. The characteristic strengths of the concrete and steel are fck = 30 N/mm2. Effective depth, d=434mm and breadth = 400mm.
Permanent load, gk = 40 kN/m (including self weight)
Variable load, qk = 20 kN/m
Ultimate loading and maximum moment
Ultimate load, wu = (1.35gk + 1.5qk) kN/m
= (1.35 x 40 + 1.5 x 20) = 84 kN/m
therefore
maximum design moment M = \(\frac{w_uL^2}{8} = \frac{84\times 6.25^2}{8} = 410 kNm\)
Bending Reinforcement
\(K=\frac{M}{bd^2f_{ck}} = \frac{410 \times 10^6}{400×434^2 \times 30}= 0.181 >K_{bal} = 0.167\) . Therefore, compression reinforcement, A’s is required.
d’/d = 60/434 = 0.138 < 0.171, therefore fsc = 0.87 fyk.
Compression steel:
\(A’_s\frac{(K-K_{bal})f_{ck}bd^2}{f_{sc}(d-d’)}\)
\(=\frac{(0.181-0.167) \times 30 \times 400 \times 434^2}{0.87 \times 500(434-60)} = 190 mm^2\)
Provide 2H16 bars, A’s = 402 mm2.
Tension steel, \(A_s=\frac{0.167f_{ck}bd^2}{0.87f_{yk}z_{bal}} + A_s’\)
where, from the lever arm curve, la = 0.82.
Thus,
\(A_s = \frac{0.167\times 30 \times 400 \times 434^2}{0.87\times 500 \times (0.82 \times 434)} + 190\)
\(= 2438 + 190 =2628mm^2\).
Provide 4 H32 bars, area = 3217 mm2.
Span-effective depth ratio
\(\rho = 100A_{s,req}/bd = (100\times 2628)/(400\times 434) = 1.51%\)
From span-ratio table, basic span/effective depth for a simply supported beam is 14.
Modification for ratio = 14 x (3217/2628) = 17.14
Span-effective depth ratio provided = 6250/434 = 14.4.
14.4<17.14 .. Therefore, it is okay.