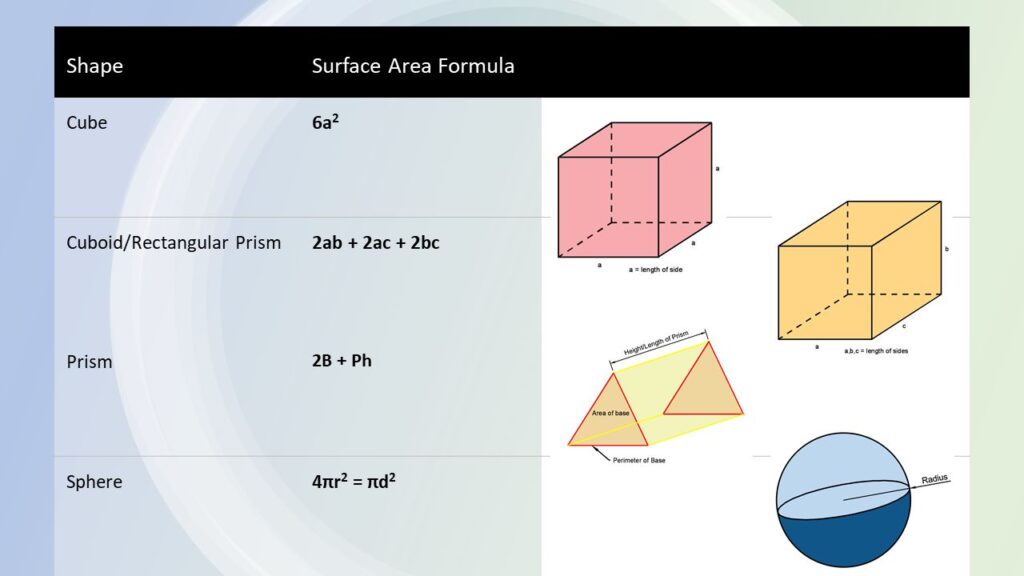
Summary of Surface Areas of Common Shapes
Table of Contents
Formula for Surface Area
The formula for surface area is the sum of all the areas of a shape that covers the surface of an object.
An example is a cube shape, which has 6 sides. The surface area of the cube is the sum of all six sides.
This page goes over the surface area of the following shapes:
- Cuboid
- Rectangular Prism
- All Prisms
- Sphere
- Cylinder
- Pyramid
- Cone
In the formulas below, the notations “a“, “b” and “c” all refer to lengths. “a” is a different length to “b“, which is also different to “c“. We are using these notations instead of actual numbers, so we can create a formula and input the values into the specific formula of surface area of a shape.
The term “ab” means “a” multiplied by “b“. “a2” means “a squared” or ” a multiplied by a“.
Important note – make sure the units of the sides are all the same when carrying out calculations.
Surface Area of a cube
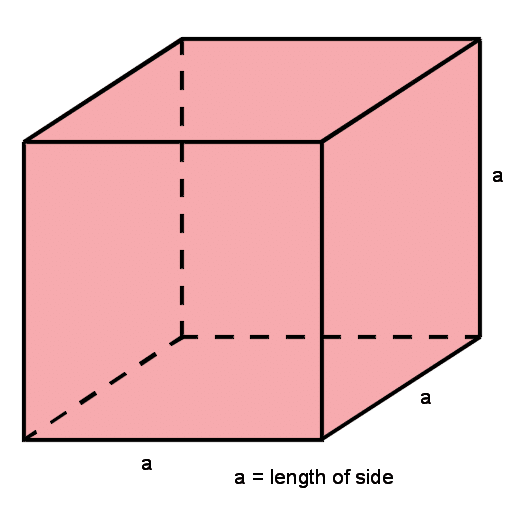
The surface area of a cube is the sum of the areas of all six sides. All lengths of the cubes are the same.
The area of a single side is a x a, or it can be shown as a2.
As there are six sides, we can make the formula for the surface area of a cube as 6a2.
Formula for Surface area of a cube = 6a2
Surface Area of a Rectangular Prism or Cuboid
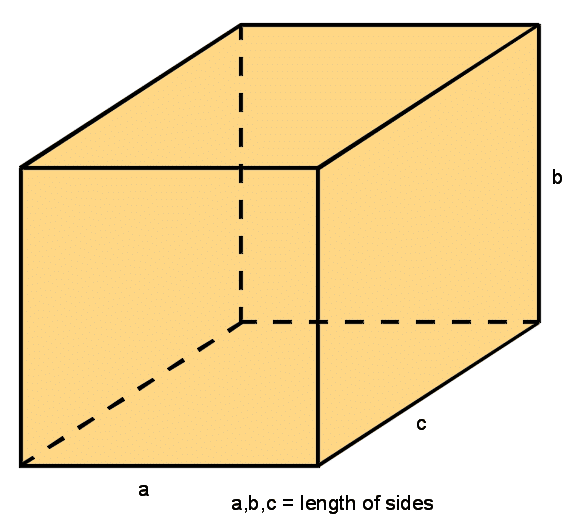
The surface area of a rectangular prism is the sum of the areas of all six sides. All sides of the Prism are right angles, which makes the opposite faces of the cuboid equal.
In this shape, the opposite side have the same area (top and bottom face are equal, front and back face are equal, left and right sides are equal).
a = length, b = height, c = width
Front and Back face:2ab
Top and bottom face: 2ac
Side face: 2bc
The combined area is 2ab + 2ac + 2bc
Surface area of a Rectangular Prism = 2ab + 2ac + 2bc
Surface Area of any Prism
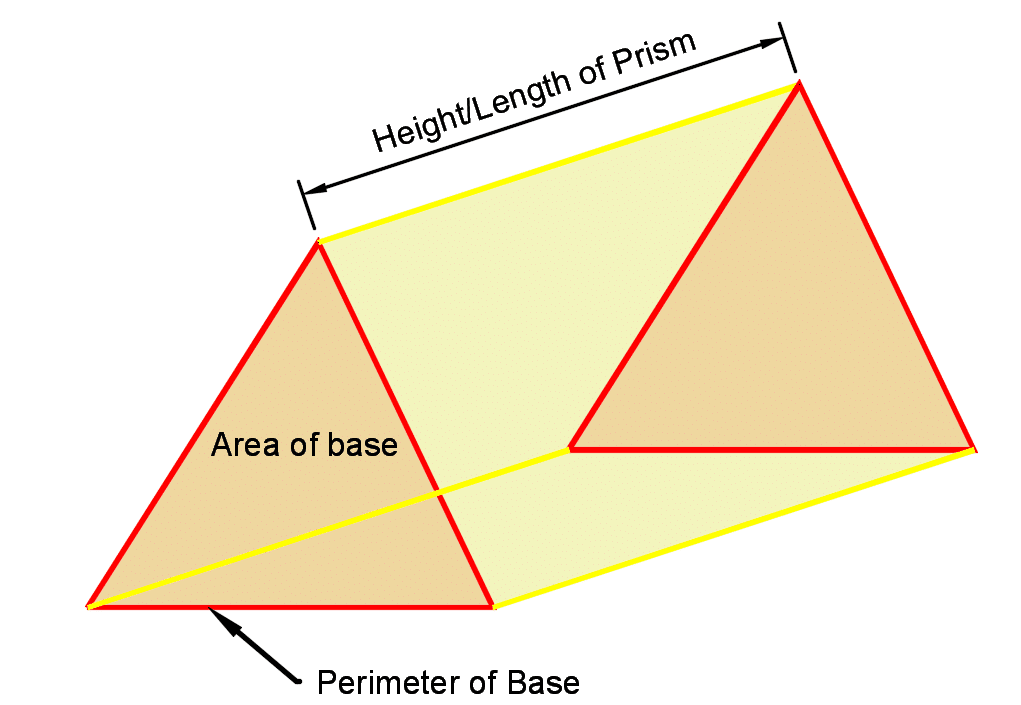
A prism is a solid object with identical ends, flat faces and has the same cross-section along its length. (cylinders are not prisms)
In this shape, the area of the base at both ends are identical, giving 2B (B is base area)
B = area of base, P = perimeter of one base, h = height
The area of the faces is the perimeter of one base multiplied by the height, giving us Ph.
The combined area is 2B + Ph
Formula for Surface area of a Prism = 2B + Ph
Surface Area of a Sphere
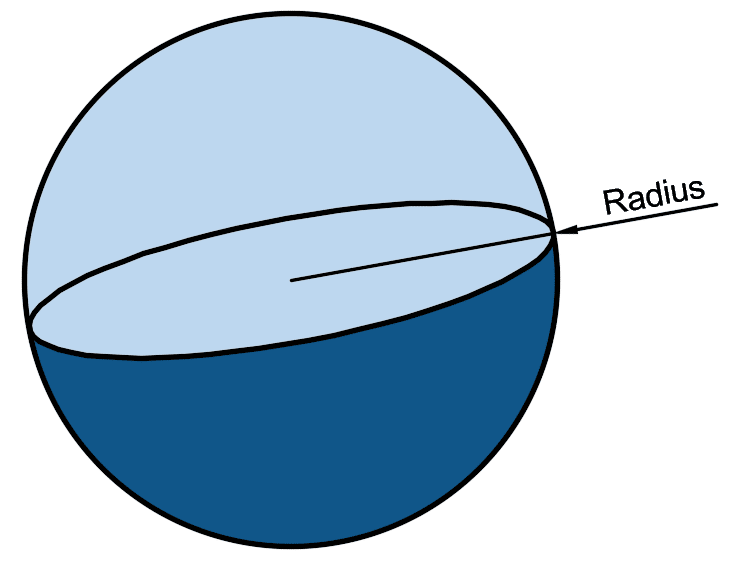
A sphere is an object that is the surface of a ball.
The surface area is calculated using the radius of the circle.
Formula for Surface area of a Sphere = 4πr2 = πd2
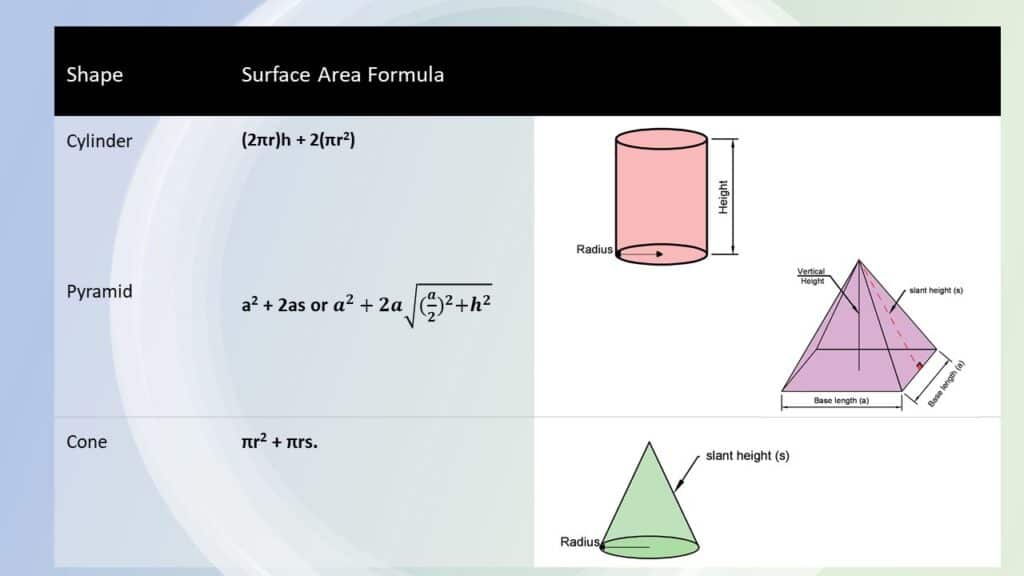
Surface Area of a Cylinder
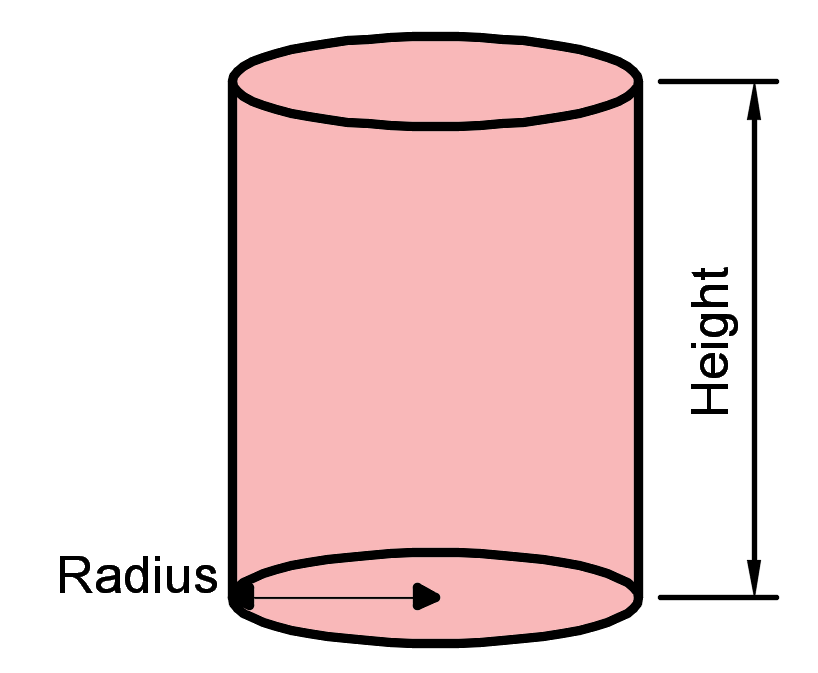
A cylinder is a cylindrical object with two circular flat ends and one curved side. It has the same cross-sectional area along the length of the shape.
The surface area is the sum of the areas of each end and curved surface
Surface area of both ends = 2πr2
Surface of curved surface = 2 π rh
Total surface area = 2 π rh + 2πr2
Formula for Surface area of a cylinder = (2*π*r)*h + 2(π*r2)
Surface Area of a Pyramid
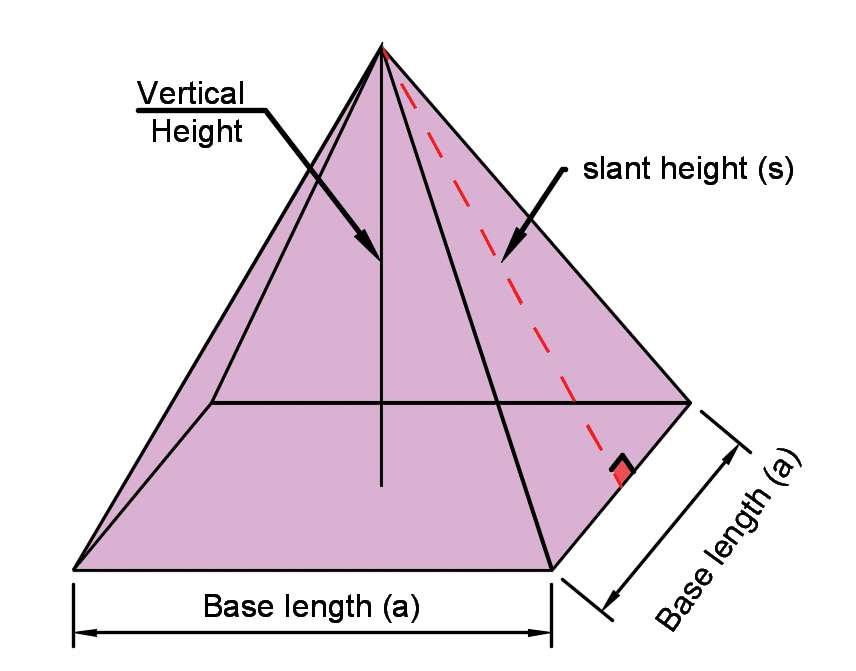
A square shaped pyramid has a square base and triangular faces on each side.
The area of the base will be a x a = a2 (area of square)
The surface area is the sum of the areas of the base and all sides.
The surface area of the pyramid sides is the determined through the slant (s) height and base length (a). (area of a triangle is 1/2 x base x height, as there are 4 sides, the total area of the sides are 2*a*s) .
Total surface area = a2 + 2*a*s
If we have the vertical height of the pyramid, this can be \(a^2 + 2a \sqrt {(a/2)^2 + h^2}\)
Surface area of a Pyramid = a2 + 2*a*s or \(a^2 + 2a \sqrt {(a/2)^2 + h^2}\)
Surface Area of a Cone
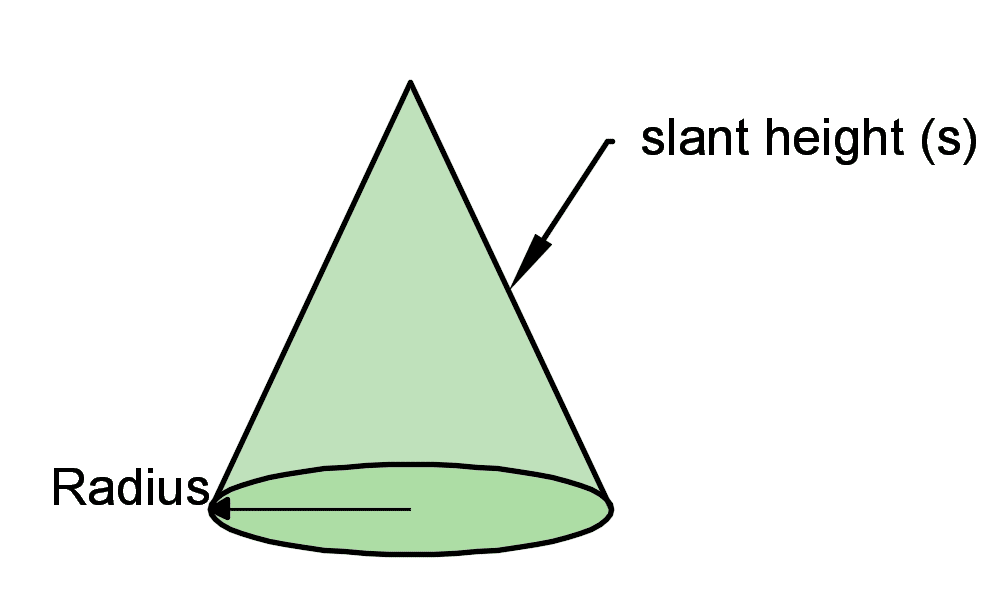
A cone is made up of one curved side and base (circular base). A classic example is an ice cream cone.
The area of the base will be πr2 (area of circle).
The surface area of the curved side is π*r*L.
The total surface area of the cone will be πr2 + π*r*L.
Formula for Surface area of a Cone = πr2 + π*r*L.