Civil's Guide
Useful Engineering Equations
Bending and deflection formulas
When designing beams (concrete, steel or timber), the bending and shear capacity is checked against applied bending theory. An applied force causes the element to bend and it is subjected to bending moments and ends react to shear loads.
The bending and shear profile of a beam/element depends on the type of beam support (i.e, pinned, fixed and free ends).
Elastic bending formula
\(\frac{M}{I}=\frac{\sigma}{y}=\frac{E}{R}\)
- M is the applied moment
- I is the section moment of inertia
- \(\sigma\) is the fibre bending stress
- y is the distance from the neutral axis to the fibre and R is the radius of curvature
- Section modulus is Z=I/y
- Applied bending stress can be simplified to \(\sigma\) = M/Z
Typical Beam design
An example of designing any beam can be simplified in the steps below:
- Determine the support conditions (fixed or pinned).
- Calculate the load applied to the beam.
- Calculate the bending moment and shear force in the beam based on typical diagrams below.
- Check applied bending moment and shear against required Eurocode or relevant codes (i.e, bending capacity, shear capacity)
Typical Bending and deflection formulas
Loading
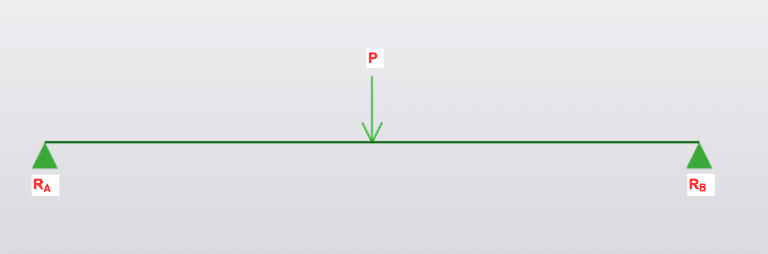
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{midspan} = \frac{PL}{4}\)
Deflection:
\(\delta = \frac{PL^3}{48EI}\)
Shear Force
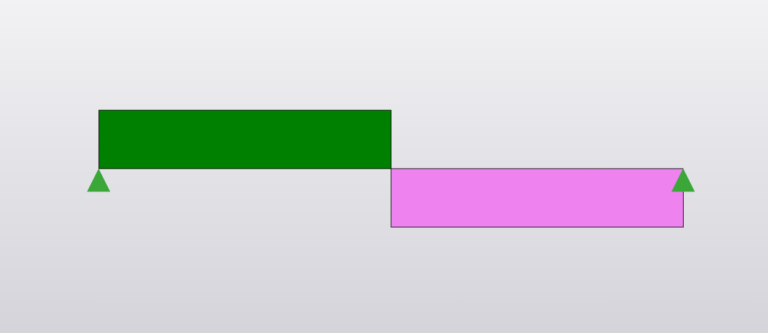
Reaction:
\(R_A=R_B=\frac{P}{2}\)
Loading
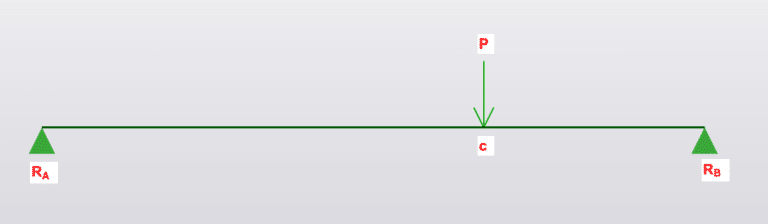
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{C} = \frac{Pab}{L}\)
Deflection:
when a>b,
\(\delta_x = \frac{Pab(L+b)}{27EIL} \sqrt{3a(L+b)}\)
at \(x=\sqrt{\frac{a(L+b)}{3}}\) from A
Shear Force
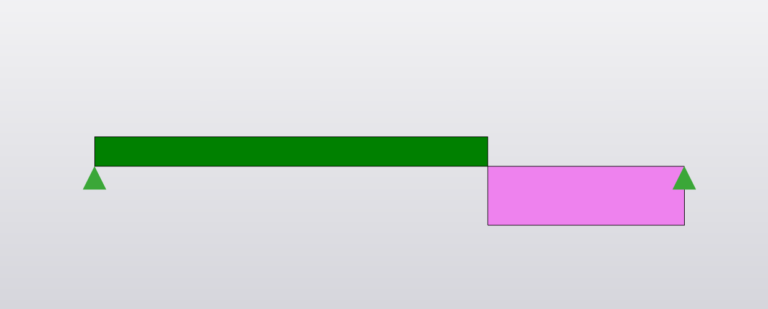
Reaction:
\(R_A= \frac{Pb}{L}\)
\(R_B= \frac{Pa}{L}\)
Loading
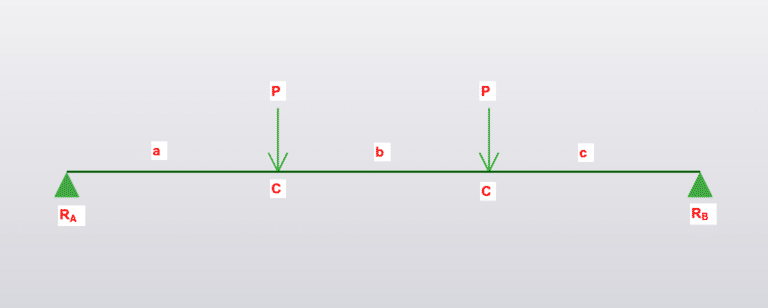
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{C} = Pa\)
\(M = \frac{PL}{3}\)
Deflection:
when a>b,
\(\delta_{midspan} = \frac{PL^3}{6EI} (\frac{3a}{4L}-(\frac{a}{L})^3)\)
\(\delta = \frac{23PL^3}{648EI}\)
Shear Force
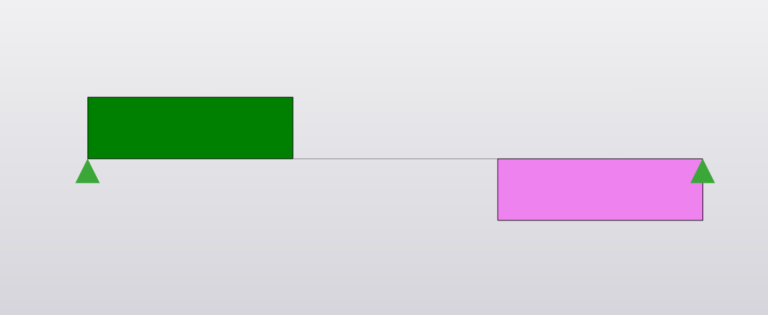
Reaction:
\(R_A = R_B = P\)
Thirdpoins: \(a=\frac{L}{3}\)
Loading
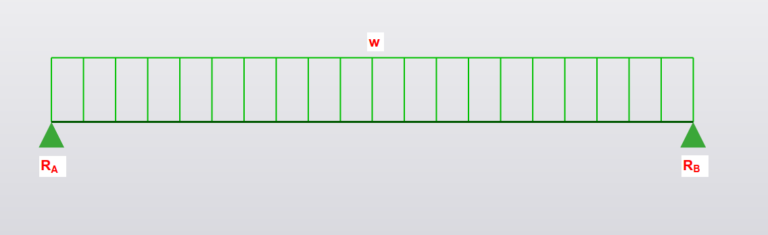
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{midpan} = \frac{wl^2}{8}\)
Deflection:
\(\delta_{midspan} = \frac{5wl^4}{384EI} \)
Shear Force
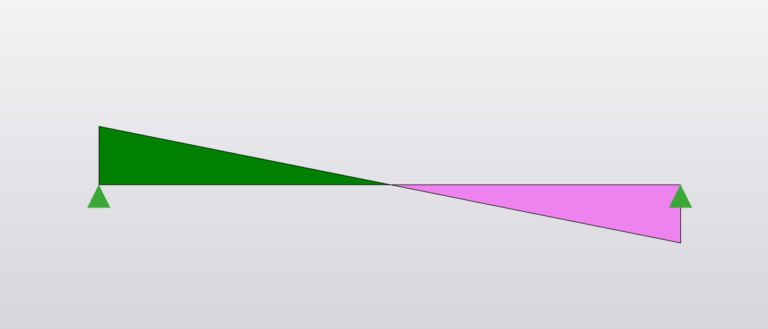
Reaction:
\(R_A = R_B = \frac{wL}{2}\)
Loading
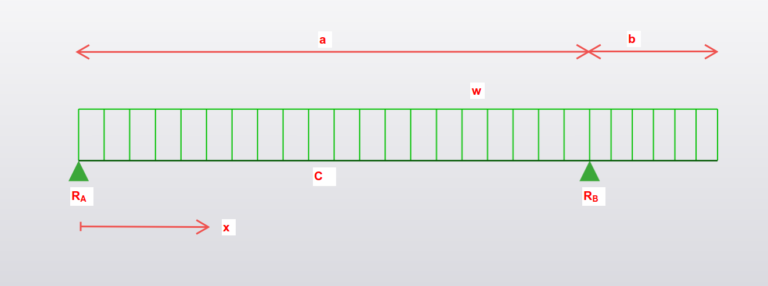
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{B} = \frac{wb^2}{2}\)
\(M_{C} = \frac{w(a+b)^2(a+b)^2}{8a^2}\)
maximum x = \(\frac{a}{b}(1-\frac{b^2}{a^2}\)
Deflection:
\(\delta_{c} = \frac{wL}{24EI}(x^4-2ax^3+\frac{2b^2}{a}x^3+a^3x-2ab^2x) \)
\(\delta_{freetip} = \frac{wb}{24EI}(3b^3 + 4ab^2-a^3) \)
Shear Force
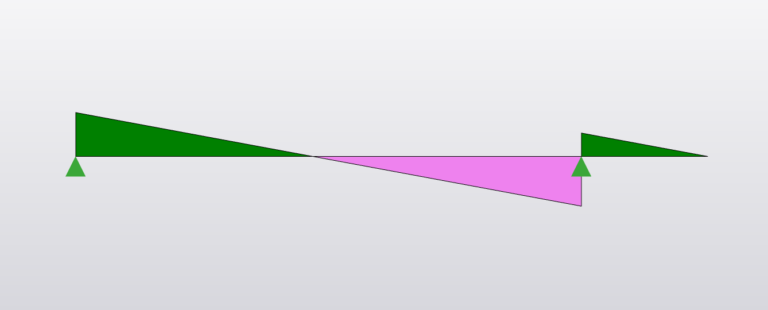
Reaction:
\(R_A = \frac{wL}{2a}(a^2-b^2)\)
\(R_B = \frac{wL}{2a}(a^2+b^2)\)
Loading
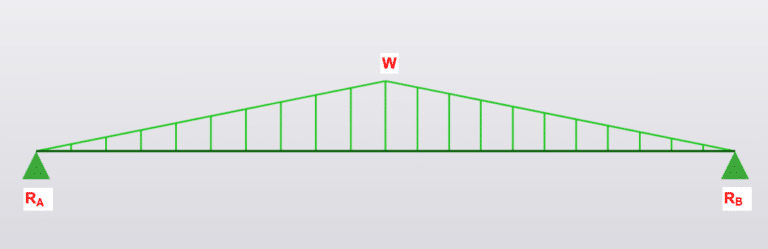
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{Midspan} = \frac{WL}{6}\)
Deflection:
\(\delta_{midspan} = \frac{WL^3}{60EI}\)
Shear Force
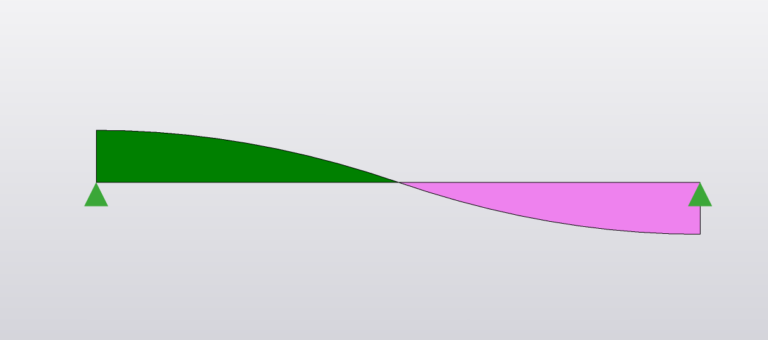
Reaction:
\(R_A = R_B = \frac{W}{2}\)
Loading
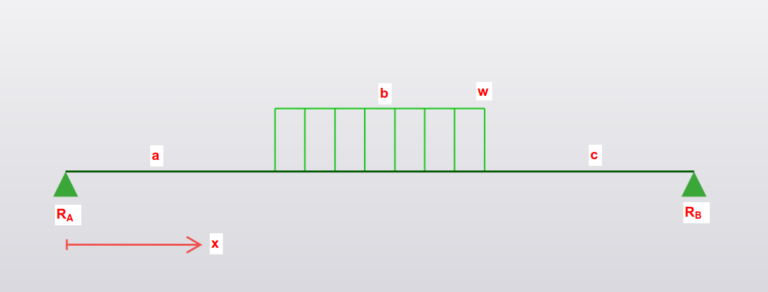
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{Max} = \frac{W}{b}(\frac{x_1^2-a^2}{2})\)
When \(x_1=a+\frac{R_Ab}{W}\)
Deflection:
\(\delta_{max} = \frac{W}{384EI}(8L^3-4Lb^2+b^3)\)
Shear Force
Reaction:
\(R_A = \frac{W}{L} (\frac{b}{2}+c)\)
\(R_B = \frac{W}{L} (\frac{b}{2}+a)\)
Loading

- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{x} = \frac{Wx(L^2-x^2)}{3L^2}\)
maximum at x=0.5774L
Deflection:
\(\delta_{midspan} = \frac{5WL^3}{384EI}\)
\(\delta_{max} = \frac{0.01304WL^3}{EI}\)
when x = 0.5193L
Shear Force
Reaction:
\(R_A = \frac{W}{3}\)
\(R_B = \frac{2W}{3}\)
Loading
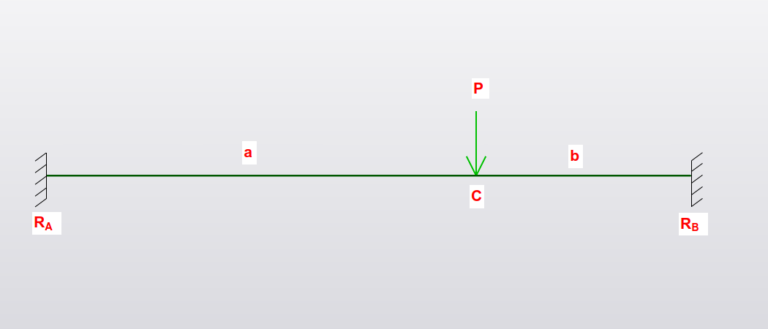
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{A} = \frac{-Pab^2}{L^2}\)
\(M_{B} = \frac{-Pba^2}{L^2}\)
\(M_{C} = \frac{2Pa^2b^2}{L^3}\)
Deflection:
\(\delta_{max} = \frac{2Pa^3b^2}{3EI(L+2a)^2}\)
when \(x=\frac{L^2}{(3L-2a)}\)
\(\delta_{c} = \frac{Pa^3b^2}{3EIL}\)
Shear Force
Reaction:
\(R_A = \frac{Pb^2(L+2a)}{L^3}\)
\(R_B = \frac{Pb^2(L+2b)}{L^3}\)
Loading
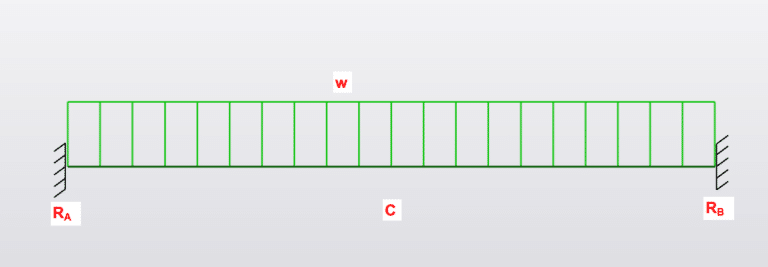
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{A} = M_{B} = \frac{-wL^2}{12}\)
\(M_{C} = \frac{wL^2}{24}\)
Deflection:
\(\delta_{midspan} = \frac{wL^4}{384EI}\)
Shear Force
Reaction:
\(R_A = R_B \frac{wL}{2}\)
Loading
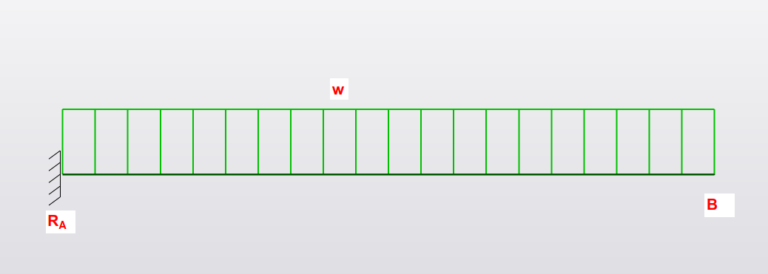
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{A} = \frac{-wL^2}{2}\)
Deflection:
\(\delta_{B} = \frac{wL^4}{8EI}\)
Shear Force
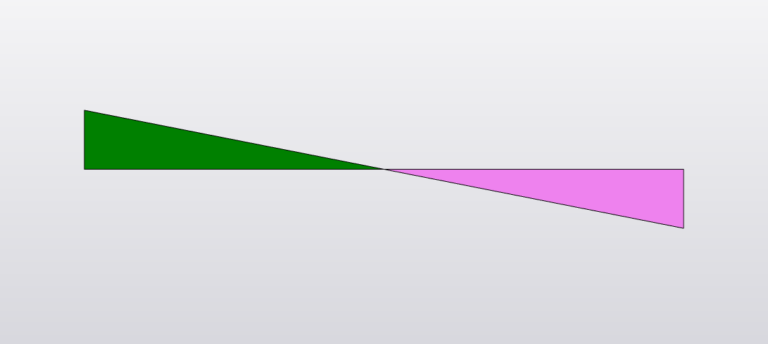
Reaction:
\(R_A = wL\)
Loading
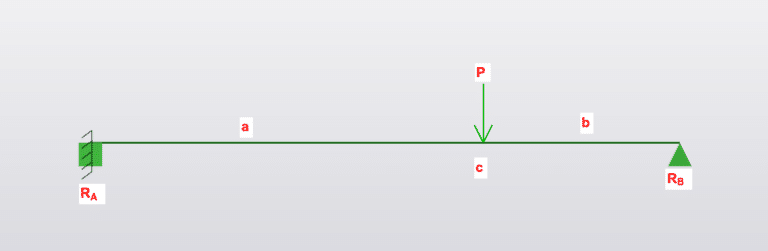
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{A} = \frac{-Pb(L^2-b^2)}{2L^2}\)
\(M_{C} = \frac{Pb}{2}(2-\frac{3b}{L}+\frac{b^3}{L^3}\)
Deflection:
\(\delta_{c} = \frac{Pa^3b^2}{12EIL^3}(4L-a)\)
Shear Force
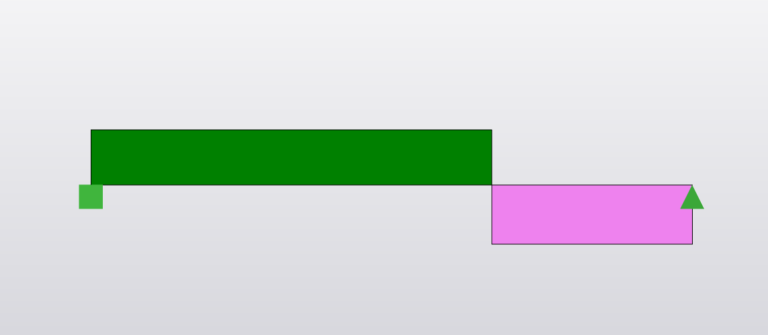
Reaction:
\(R_A = P-R_B\)
\(R_B = \frac{Pa^2(2L+b)}{2L^3}\)
Loading
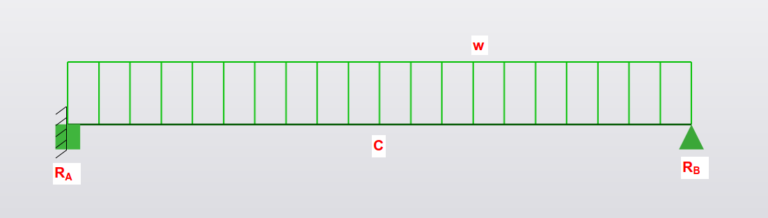
- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{A} = \frac{wL^2}{8}\)
\(M_{sagging} = \frac{9wL^2}{128}\) at 0.62L from A
Deflection:
\(\delta_{max} = \frac{wL^4}{185EI}\) at 0.58L from A
Shear Force
Reaction:
\(R_A = \frac{5wL}{8}\)
\(R_B = \frac{3wL}{8}\)
Loading

- P is Force in kN
- L is total length in mm
- E is young’s modulus
- I is the second moment of area (\(mm^2\))
- W is total load (UDL x length)
- w is UDL (force per unit length, kN/m)
Maximum moment and deflection

Moment:
\(M_{A} = \frac{Pb}{2}\)
\(M_{B} = -Pb = -2M_A\)
Deflection:
\(\delta_{c} = \frac{Pab^2}{4EI}(a+\frac{4b}{3})\)
Shear Force

Reaction:
\(R_A = \frac{-3Pb}{2a}\)
\(R_B = \frac{P}{a}(a+\frac{3b}{2}\)
