Concrete Superstructure : Slab Design
Table of Contents
Continuous Spanning Slab Design
Concrete slabs are either two way spanning or one way spanning slab. A continuous spanning slab is a type of reinforced concrete slab which is commonly used in construction which is supported on primary beams or a supporting walls. This article will cover a one way continuous spanning slab design example, checking over a reinforcement details.
Continuous spanning slabs have a lower thickness in comparison to simply supported slabs. This is useful in achieving thinner slabs, especially in areas which require greater floor to ceiling height.
These can be used for floors, roofs and other engineering applications. A continuous slab requires more tension reinforcement in the bottom of the slab (middle of the slab) and over the support (top reinforcement).
The steps for a continuous spanning slab design example is shown below:
- Load take-down on slab
- Preliminary design of slab
- Bending moment reinforcement
- Shear force reinforcement check
- Control crack widths for reinforced concrete
- Span – effective depth ratio
One way spanning slab design example
A continuous spanning slab is designed to undertake plant loading on the first floor .
The office loading has been taken as 7.5 kN/m2. The floor finishes, ceilings and services have been taken as 1.0 kN/m2.
The concrete grade of the slab is C32/40. The fck = 32 N/mm2 and fyk = 500 N/mm2 (yield stress of reinforcement).
Length between slab is 4.0m (centerline of support).
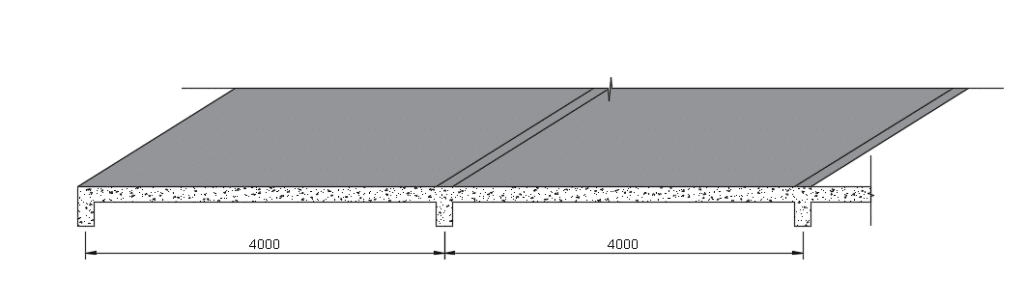
Continuous Spanning Slab Design Example - Preliminary design
The first step in the design of a continuous spanning slab is assuming the possible thickness of the slab before undertaking the detailed design. This can be done through basic span/effective depth ratio to determine the basic thickness/depth of the slab.
| Basic ratios of span/effective depth for initial design (f_{yk} = 500 MPa) | |
|---|---|
| Structural System | Span/Effective Depth Ratio |
| Slab | |
| One-way or two-way spanning simply supported slab | 20 |
| End span of: one-way/two-way contnuous spanning slab | 26 |
| Interior span of: one-way/two-way spanning slab | 30 |
| Flat slab (supported on columns) | 24 |
| Cantilever | 8 |
The span/depth ratio = 26 for a continuous spanning slab.
4500/depth = 26, therefore, 4500/26 = 173mm
Therefore, we will design a 200mm thick slab.
The cover to the slab has been taken as 30mm. (Assume that the slab in internal with an XC1 exposure class). Assume a bar diameter of 12mm.
Effective depth of slab = 200 – 30 – 12/2 = 164mm
Slab Loading
Slab self-weight = 0.20 x 25 kN/m3 = 5.0 kN/m2
Finishes = 1.0 kN/m2
Permanent Load = 6.0 kN/m2
Imposed/Variable Load = 7.5 kN/m2
The slab will be designed in 1m strips
Bending Reinforcement Design
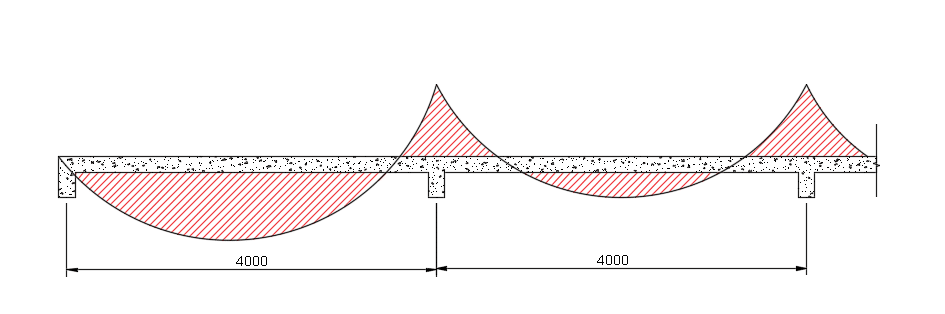
Continuous spanning slabs results in moments above the support and middle of the spans, which requires a moment frame analysis.
Generally, coefficients are used to calculate the bending moment over the span areas and are listed below:
Using the coefficient to determine the moment for at the middle of the interior spans.
F = (6.0 x 1.35 + 7.5 x 1.5) x 4 = 77.4 kN
Therefore, M = 0.086Fl = 0.080 x 77.4 x 4.0 = 27 kNm
Bending reinforcement
K = M/bd2fck = (27 x 106)/(1000 x 1642 x 32) = 0.032 < 0.167, no compression is required
From the lever-arm curve, la can be determine or z = d[0.5 + √(0.25-K/1.134)]
\(z = 164[0.5 +\sqrt 0.25 – 0.032/1.134] = 159mm\), check if this is less than 0.95d (0.95 x 164 = 156mm)
\(A_s = \frac{M}{0.87f_{yk}z}\) = (27 x 10^6)/(0.87 x 500 x 156) = 400 mm2/m
Therefore, provide B12 bars @ 150mm c/c, As = 754 mm2.
| Outer Support |
Near middle of end span |
At first interior support |
At middle of interior span |
At internal supports |
|
|---|---|---|---|---|---|
| Moment | -0.04Fl | 0.086Fl | -0.086Fl | 0.063Fl | -0.063Fl |
| Shear | 0.460F | - | 0.60F | - | 0.5F |
Shear Design
Shear force at the internal supports are 0.60 F
(1.35 x 6.0 + 1.5 x 7.5) x 4.0 x 0.60 = total force on beam.
Shear, Ved = 46.5 kN
Ved/bd = (46.5 x 103)/(1000 x 164) = 0.28 N/mm2
\(\rho\) = 100 x 754/ (1000 x 164) = 0.46%
\(V_{rdc} = v_{rdc}bd\) where
\(v_{rd,c} = [0.12k \times (100 \times \rho \times f_{ck})^{1/3}] \)
where \(K = 1+ \sqrt{200/d}\)
where \(K = 1 + \sqrt{200/164} = 2.1\)
However, K is limited to 2.0
\(v_{rd,c} = [0.12 \times 2.0 \times (100 \times 0.0046 \times 32)^{1/3}] = 0.59 N/mm^2 \)
\(v_{min} = 0.035 \times k^{3/2} \times f_{ck}^{1/2}\)
\(v_{min} = 0.035 \times 2.0^{3/2} \times 32^{1/2} = 0.56 N/mm^2\)
vrdc > ved …OKAY
No shear reinforcement is required
Check Bars Stress
Stress in reinforcement can be checked through the equation below:
\(\sigma_s = \frac{f_{yk}}{\gamma_{ms}} \frac{\psi_2 Q_k + G_k}{1.5Q_k + 1.35 G_k} \frac{A_{s,req}}{A_{s,prov}} \frac{1}{\delta}\)
where \(\psi_2\) can be taken from the table NA.A1.1, which contains values for buildings.
\(\delta\) can be taken as 1.0
\(\frac{f_{ck}}{\gamma_{ms}}\) = 435 for 500 MPa reinforcement.
| Alternative requirements to control crack widths to 0.3mm for members reinforced with high bond bars | |
|---|---|
| Maximum bar diameter (mm) |
Stress range (MPa) |
| 40 | 150-165 |
| 32 | 165-190 |
| 25 | 190-210 |
| 20 | 210-230 |
| 16 | 230-260 |
| 12 | 260-290 |
| 10 | 290-320 |
| 8 | 320-360 |
| Alternative requirements to control crack widths to 0.3mm for members reinforced with high bond bars | |
|---|---|
| Maximum bar spacing (mm) |
Stress range (MPa) |
| 300 | \(\leq\) 160 |
| 275 | 160-180 |
| 250 | 180-200 |
| 225 | 200-220 |
| 200 | 220-240 |
| 175 | 240-260 |
| 150 | 260-280 |
| 125 | 280-300 |
| 100 | 300-320 |
| 75 | 320-340 |
| 50 | 340-360 |
Stress in reinforcement can be checked through the equation below:
\(\sigma_s = 435 \frac{1.0 \times 7.5 + 6.0}{1.5 \times 6.0+ 1.35 \times 7.5} \frac{400}{754} = 165 MPa\)
We can check the 165 MPa on either the two tables. The maximum bar spacing can be taken as 275mm.
We have chosen a bar spacing of 200mm, which is less than 275mm.
Span - effective depth ratio
The actual span/ effective depth = (4000)/164 = 24.4
\(\rho = \frac{100A_s}{bd} = \frac{100 \times 754}{1000 \times 164} = 0.46%\)
The allowable span/effective depth from the table below is 30 (we can interpolate but we will use the lower value for simplicity).
\(\frac{A_{s,prov}}{A_{s,req}} = \frac{754}{400} = 1.885\)
The allowable span/effective depth x 1.885 = 30 x 1.885 = 56.55 > 24.4
| Span/effective depth ratios for slabs | |||
|---|---|---|---|
| Location |
\(\frac{A_{s,req}}{bd} \geq 1.5%\) |
\(\frac{A_{s,req}}{bd} = 0.5%\) |
\(\frac{A_{s,req}}{bd} \leq 0.35%\) |
| One-or two way spanning slab: Simply supported End span Interior span |
|||
| 14 | 20 | 30 | |
| 18 | 26 | 39 | |
| 20 | 30 | 45 | |
| Flat slab | 17 | 24 | 36 |
| Cantilever | 6 | 8 | 12 |
